Aufgabe:
"Wenn C gegeben ist, dann sind T und A voneinander unabhängig."
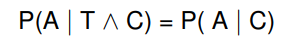
In diesem Fall kann die Evidenz schrittweise durch eine einfache iterative Methode hinzugefügt werden. Gemäß dem Satz von Bayes:
Text erkannt:
\( P(A \mid T \wedge C)=P(A \mid C) \)
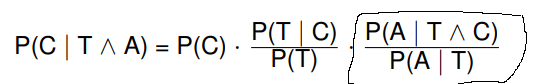
Text erkannt:
\( P(C \mid T \wedge A)=P(C) \cdot \frac{P(T \mid C)}{P(T)} \cdot \frac{P(A \mid T \wedge C)}{P(A \mid T)} \)
Problem/Ansatz:
ich lerne gerade das Bayes Theorem und habe gerade Probleme mit dieser "Update-Funktion" P(C| T und A), ich verstehe es so, dass wir hier die a priori Wahrscheinlichkeit P(C) aktualisieren wollen mittels der rechten Formel. Jetzt verstehe ich nicht, wieso wir den letzten bzw. umkreisten Term hinzufügen, woher kommt dieser ?