Quadratische Ungleichung lösen

Question

Aufgabe:

Ich habe zwei Quadratische Funktionen

f(x)= -2x² -2x +4

g(x)= 5x² +3x

Lösen Sie Graphisch folgende Ungleichung: f(x) < g(x)

Problem/Ansatz:

Die Lösung ist doch ⇒L ] -0,5; 0 [ oder?

Aber bei g(x) > 0 komm ich nicht weiter, kann jemand weiter helfen?

Blau = g(x)

Grün = f(x)

Answer 1

Aber bei g(x) > 0 komm ich nicht weiter, kann jemand weiter helfen?

Wo willst du denn da "weiterkommen"?

Du sollst doch einfach nur angeben, für welche x die "grünen" Werte kleiner sind als die "blauen" Werte.

Das ist nach deinen beiden Graphen der Fall von -∞ bis ca. -1,2 und von (nicht ganz) 0,5 bis ∞.

Etwas genauer bekommst du die Grenzen, wenn du sie selbst durch Gleichsetzen beider Funktionen berechnest oder wenn du dir von Geogebra die Schnittpunkte beider Graphen anzeigen lässt.

Comments

von (nicht ganz) 0,5 bis ∞.

Das wäre dann g(x) < 0 oder?

---

Nein! Bei ca, 0,5 sind die Funktionswerte von f und g gleich (sie sind dort etwa 2,6 und g(x) ist dort also keinesfalls 0).

---

Was wäre dann die Lösung für g(x) < 0

Das hier: L ] 0; ∞ [ ??

Weil bei 0 hat sie ja die Nullstelle, und geht dann bis unendlich?

---

Was wäre dann die Lösung für g(x) < 0

Gegenfrage: Was hat das zu tun mit

Lösen Sie Graphisch folgende Ungleichung: f(x) < g(x)

Wenn das mit dem g(x)<0 irgendeine andere Teilaufgabe gewesen sein sollte: Geh zum Optiker deines Vertrauens und lasse dir eine Brille anfertigen.

Es ist g(x) HIER (rot markiert) kleiner als 0.

---

Es ist g(x) HIER (rot markiert) kleiner als 0.

Bedeutet g(x) < 0 nicht größer als 0?

---

Bedeutet g(x) < 0 nicht größer als 0?

Nein.

g(x) größer als 0 würde so geschrieben:  g(x)>0.

---

Bedeutet g(x) < 0 nicht größer als 0?

Nein.
g(x) nicht größer als 0 würde so geschrieben: g(x)≤0.

Answer 2

-2x^2-2x+4 < 5x^2+3x

-7x^2-5x+4 <0

x^2+5/7*x-4/7 >0

Nullstellen mit pq-Formel:

-5/14+-√(25/196+4/7) = -5/14+-√137/196) = -5/14+-1/14* √137

x1= -5/14+√137/14

x2= -5/14-√137/5

(x+5/14-√137/14)*(x+5/14+√137/14) = a*b

1.Fall :

a<0 u. b<0

2.Fall:

a>0 u. b>0

Wegen der Wurzeln ist die Aufgabe nicht sehr angenehm ohne Technik.

https://www.wolframalpha.com/input?i=-2x%5E2-2x%2B4+%3D5x%5E2%2B3x

Comments

Der Übergang von dieser Zeile

-7x²-5x+4 <0

zu dieser Zeile

x²+5/7*x-4/7 <0

ist falsch.

Answer 3

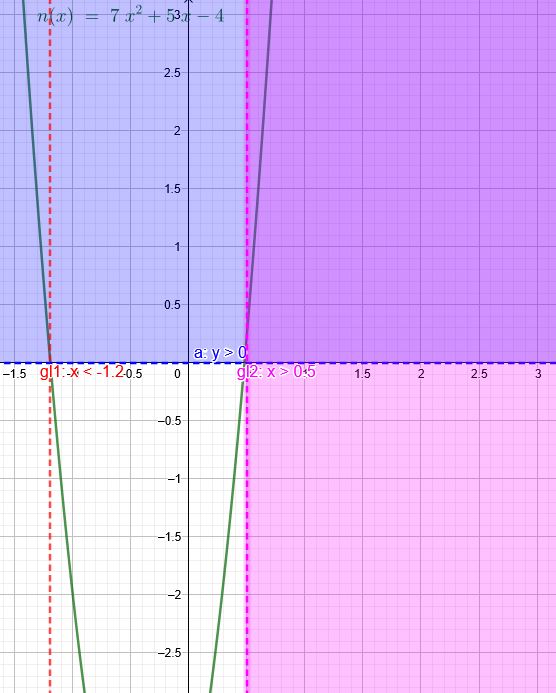
\(f(x)= -2x^2 -2x +4\)      \(g(x)= 5x^2 +3x\)        \(f(x)<g(x)\)   →   \(g(x)>f(x)\)

Lösungsweg, falls Rechnung verlangt ist:

\( 5x^2 +3x> -2x^2 -2x +4 |+ 2x^2 +2x\)

\( 5x^2 + 2x^2 +2x+3x> 4 \)

\( 7x^2+5x> 4 |:7\)

\( x^2+\frac{5}{7}x+(\frac{5}{14})^2> \frac{4}{7}+(\frac{5}{14})^2\)

\( x^2+\frac{5}{7}x+\frac{25}{196}> \frac{4}{7}+\frac{25}{196}\)

\( (x+\frac{5}{14})^2> \frac{112}{196}+\frac{25}{196}=\frac{137}{196} | \pm\sqrt{~~}\)

1.)

\( x+\frac{5}{14}>\frac{\sqrt{137}}{14} \)

\( x_1>-\frac{5}{14}+\frac{\sqrt{137}}{14}≈0,5 \)

2.)

\( x+\frac{5}{14}<-\frac{\sqrt{137}}{14} \)

\( x<-\frac{5}{14}-\frac{\sqrt{137}}{14} ≈-1,2\)

Comments

Lösungsweg, falls Rechnung verlangt ist:

Wenn in der Aufgabe steht "graphisch", dann wohl eher nicht.