Wie stelle ich eine quadratische Funktion dazu?

Question

Aufgabe:

1)Geben sie eine quadratische Funktion an, die ihren hochpunkt bei H(5/0) hat

2)Stellen Sie eine Potenzfunktion 3. Grades auf, die bei xE = 1 eine Extremstelle hat.

Problem/Ansatz:

Was muss ich machen?

Soll ich die Scheitelpunktform einsetzen?

Answer 1

Bei 1) kannst du die Scheitelpunktfunktion nutzen, denn eine quadr. Funktion hat ihren Extrempunkt im Scheitelpunkt. Achte darauf, dass deine Parabel die richtige Öffnung hat (Streckfaktor).

Bei 2) Bei x=1 soll eine Extremstelle sein. Die erste Ableitung ist an dieser Stelle also 0. Wie könnte dann die erste Ableitung aussehen? Kannst du dann von dieser Ableitung auf die eigentliche Funktion 3. Grades schließen? Ggf. die hinreichende Bedingung prüfen, ob auch tatsächlich an der Stelle ein Extremum vorliegt.

Answer 2

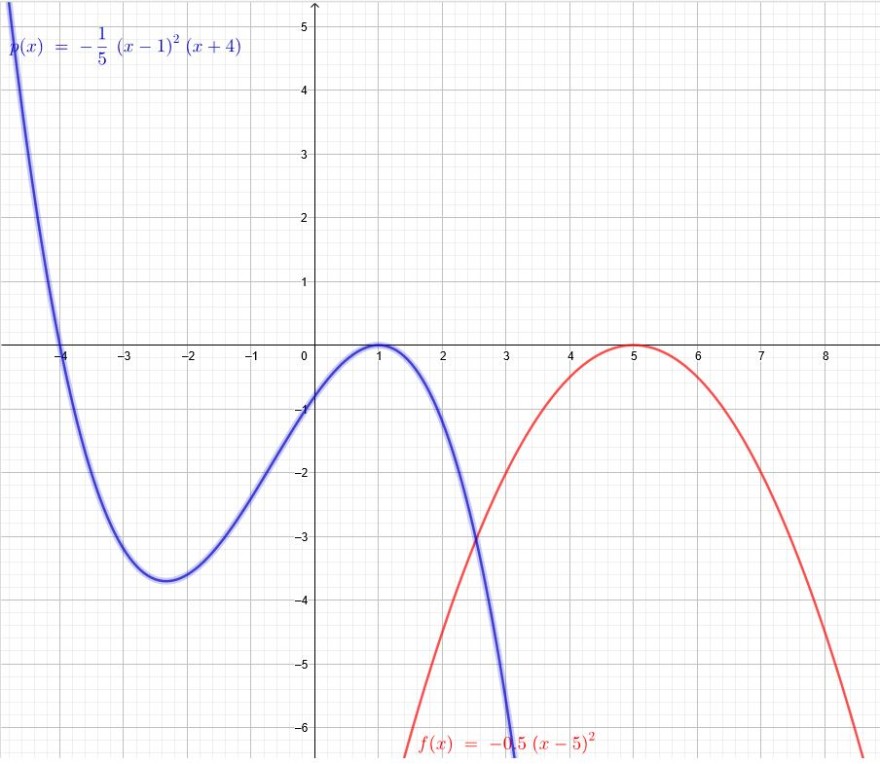
1)Geben sie eine quadratische Funktion an, die ihren Hochpunkt bei \(H(5|0)\) hat.

\(f(x)=-a\cdot(x-5)^2\)  Der Faktor a ( aber mit \(a >0\) ) kann nun verschiedene Werte annehmen.

In der Zeichnung in rot habe ich \(a=-0,5 \) gewählt.

2)Stellen Sie eine Potenzfunktion 3. Grades auf, die bei \(x_E = 1\) eine Extremstelle hat.

\(p(x)=a\cdot(x-1)^2\cdot (x-N)\)

Sowohl der Faktor a wie auch die 2.Nullstelle können nun verschiedene Werte annehmen.

In der Zeichnung in blau habe ich \(a=-\frac{1}{5} \) und N an der Stelle \(x=-4\) gewählt.

Es können nun noch \(f(x)\) und \(p(x)\) ausmultipliziert werden.

Answer 3

1) f(x) = -x^2+bx+c

f '(x)= -2x+b

f ''(x) = -2  (f ''(x) <0, Bedingung)

f(5) = 0

-25+5b+c= 0

c= 25-5b

f '(5)= 0

-10-b= 0

b= -10

c= 75

f(x) = -x^2-10x+75

2) f(x) = ax^3+bx^2

f '(x) = 3ax^2+2bx

f ''(x)= 6ax+2b

f ''(x) ≠ 0, Bedingung für Extremstelle

f '(1) = 0

3a+2b = 0

a frei wählen, a= 1

3+2b= 0

b= -1,5

f(x) = x^3 -1,5x^2

https://www.wolframalpha.com/input?i=+x%5E3+-1.5x%5E2