Zeichne dazu die Graphen f und g mit den Gleichungen

Question

Aufgabe:

Text erkannt:

Gegeben ist die lineare Gleichung
\( \frac{1}{4} x-3=3 x+3 \)
Löse die Gleichung näherungsweise graphisch. Zeichne dazu zunächst die Geraden \( \mathbf{f} \) und \( \mathbf{g} \) mit den Gleichungen:
\( f: y=\frac{1}{4} x-3 \text { und } g: y=3 x+3 \)
Lies dann die Lösung näherungsweise ab.
A - Geraden zeichnen
Zeichne zunächst die Geraden \( \mathbf{f} \) und \( \mathbf{g} \) und beschrifte sie entsprechend.

Answer 1

Hallo,

\(f: \;y=\frac{1}{4}x-3\)

Zeichne zuerst den Schnittpunkt mit der y-Achse bei (0 | -3) ein. Gehe dann 4 Einheiten nach rechts und 1 Einheit nach oben und zeichne dort den nächsten Punkt. Verbinde beide miteinander.

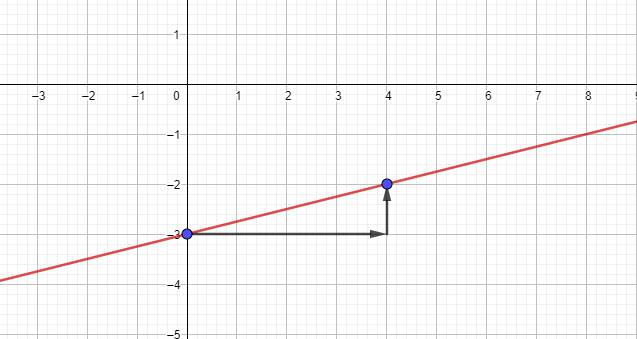
Genauso gehst du bei der anderen Geraden vor. Lies dann den Schnittpunkt ab.

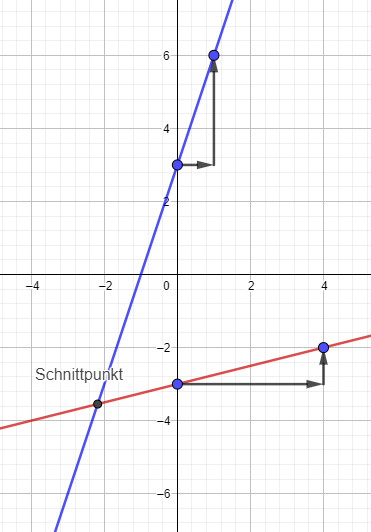
Gruß, Silvia

Answer 2

Setze jeweils 2 Punkte ein. x= 0 bietet sich an für den 1.Punkt.

Bei Brüchen zusätzlich eine Zahl, die den Bruch verschwinden lässt.

1/4*4 - 3= 1-3 = -2