Hoch- oder Tiefpunkt mit angebener Stelle bestimmen.

Question

Aufgabe:

Entscheide, ob an der angegebenen Stelle ein Hoch-,Tief- oder Sattelpunkt vorliegt.

a) 1/5*x^5-1/2*x^4      x=0

Problem/Ansatz:

Ich bin so vorgegangen:

f'(x)=x^4 - 2*x^3

f''(x)= 4*x^3 - 6*x^2

f''(0)= 0     = Sattelpunkt

Die Lösungen geben aber "Hochpunkt" als korrekte Lösung an- ich verstehe aber nicht wieso.

Danke im Voraus!

Comments

vgl:

https://www.frustfrei-lernen.de/mathematik/sattelpunkt-berechnen.html

---

Warum veröffentlichst du einen Link, in dem genau derjenige Schrott drinsteht, den ich bei S. kritisiert habe ?

---

Es ist f'(0) = f''(0) = f'''(0) = 0 und f''''(0) < 0. Es liegt ein Hochpunkt vor.

Answer 1

Hallo,

Sattelpunkte sind Wendepunkte mit waagerechter Tangente, für die diese drei Bedingungen erfüllt sein müssen:

\( \begin{array}{r}f^{\prime}(x)=0 \\ f^{\prime \prime}(x)=0 \\ f'''(x) \neq 0\end{array} \)

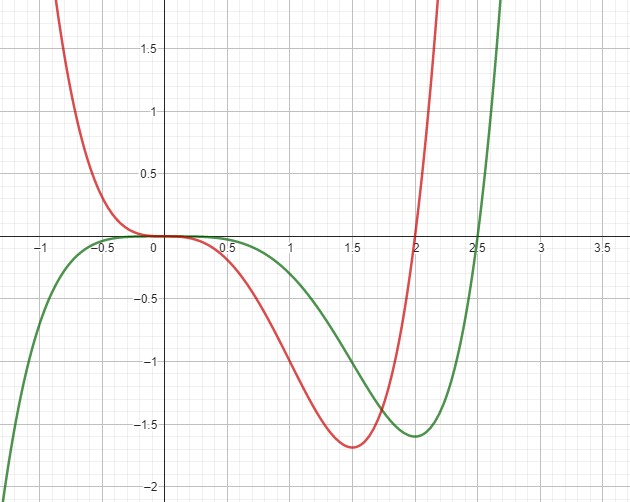
Die 3. Ableitung ist aber hier auch = 0. Der Graph von f' (rot) wechselt auch bei x = 0 das Vorzeichen von + nach -, also vor dem Punkt ist die Steigung positiv, danach negativ.

Gruß, Silvia

Comments

für die diese drei Bedingungen erfüllt sein müssen:

Ein häufig gemachter Fehler

---

Dann würde ich gerne deine fehlerfreie Version lesen.

---

Es ist einfach so, dass f'''(x) ≠ 0 nicht erfüllt sein muss.

---

Also f' = 0 und f'' = 0 muss gelten und f''' ungleich 0 kann?

Mit anderen Worten, es gibt Sattelpunkte für die f', f'' und f'''(x) = 0 sind?

---

Ja, z.B. an der Stelle x=0 bei der Funktion f mit f(x) = x^9

---

OK, danke, werde ich mir merken und am besten gleich aufschreiben...