
Text erkannt:
Aufgabe 7 (3 Punkte) Gegeben sei \( \mathbb{R}^{2} \) mit Standardkoordinatensystem \( \mathbb{E}=\left(\overrightarrow{0} ; e_{1}, e_{2}\right) \).
Darin sind die Punkte \( P_{0}, P_{1} \) und \( P_{2} \) gegeben durch:
\( { }_{\mathbb{E}} P_{0}=(2,1)^{\top}, \quad{ }_{\mathbb{E}} P_{1}=(0,-2)^{\top}, \quad{ }_{\mathbb{E}} P_{2}=(2,3)^{\top} . \)
Geben Sie ein Koordinatensystem \( \mathbb{F}=\left(Q ; f_{1}, f_{2}\right) \) an, in dem Folgendes gilt:
\( \begin{array}{c} { }_{\mathbb{F}} P_{0}=(0,0)^{\top}, \quad{ }_{\mathbb{F}} P_{1}=(1,0)^{\top}, \quad{ }_{\mathbb{F}} P_{2}=(0,1)^{\top}: \\ \mathbb{F}=(;, \end{array} \)
Geben Sie die Koordinatentransformationen \( { }_{\mathbb{E}} \kappa_{\mathbb{F}} \) und \( { }_{\mathrm{F}} \kappa_{\mathbb{E}} \) an:
\( { }_{\mathbb{E}} \kappa_{\mathbb{F}}(v)=\left(\square v+(\square), \quad{ }_{\mathrm{F}} \kappa_{\mathbb{E}}(v)=(\square+\square)\right. \)
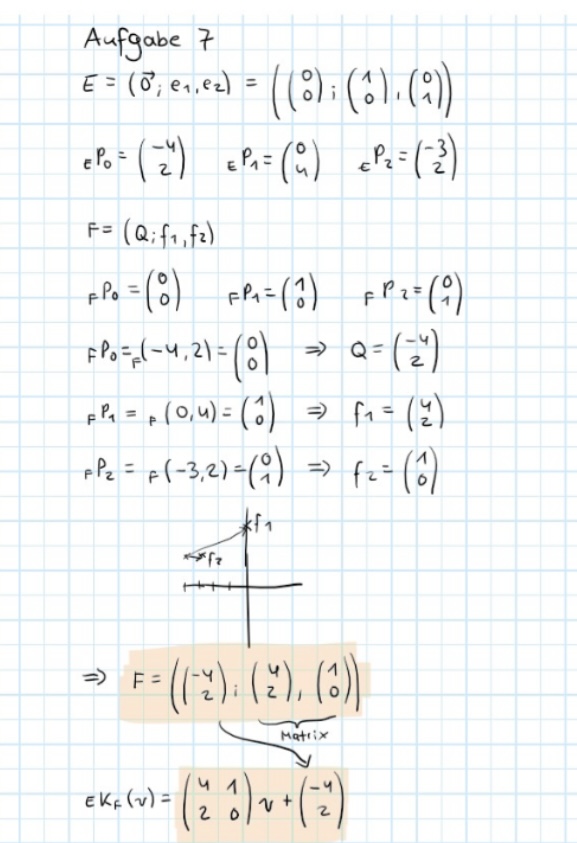
Text erkannt:
Aufgabe 7
\( \begin{array}{l} \Rightarrow F=\left(\begin{array}{c} -4 \\ 2 \end{array}\right) i \underbrace{\left(\begin{array}{l} 4 \\ 2 \end{array}\right),\left(\begin{array}{l} 1 \\ 0 \end{array}\right)}_{\text {Matrix }}) \\ E K_{F}(v)=\left(\begin{array}{ll} 4 & 1 \\ 2 & 0 \end{array}\right) v+\left(\begin{array}{c} -4 \\ 2 \end{array}\right) \\ \end{array} \)
Aufgabe:
Hallo, bei folgender Aufgabe verstehe ich nicht ganz wie vorgegangen wurde. Wie kommt man auf die einzelnen Werte. Muss man ein Koordinatensystem immer auf diese Weise bestimmen?
LG