Bin hier total lost. Bitte um Hilfe hab gar keinen Plan wie das geht.
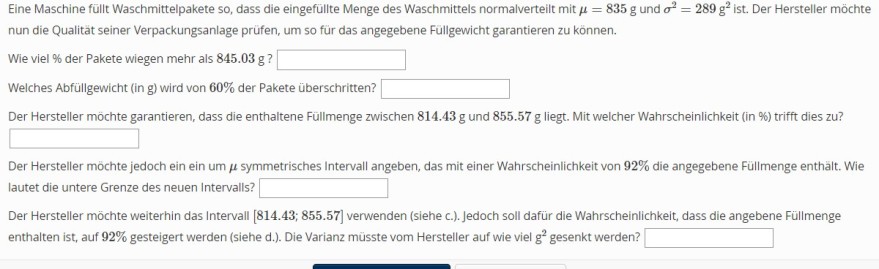
Text erkannt:
Eine Maschine füllt Waschmittelpakete so, dass die eingefüllte Menge des Waschmittels normalverteilt mit \( \mu=835 \mathrm{~g} \) und \( \sigma^{2}=289 \mathrm{~g}^{2} \) ist. Der Hersteller möchte nun die Qualität seiner Verpackungsanlage prüfen, um so für das angegebene Füllgewicht garantieren zu können.
Wie viel \% der Pakete wiegen mehr als \( 845.03 \mathrm{~g} \) ?
Welches Abfüllgewicht (in g) wird von \( 60 \% \) der Pakete überschritten?
Der Hersteller möchte garantieren, dass die enthaltene Füllmenge zwischen \( 814.43 \mathrm{~g} \) und \( 855.57 \mathrm{~g} \) liegt. Mit welcher Wahrscheinlichkeit (in \%) trifft dies zu?
Der Hersteller möchte jedoch ein ein um \( \mu \) symmetrisches Intervall angeben, das mit einer Wahrscheinlichkeit von \( 92 \% \) die angegebene Füllmenge enthält. Wie lautet die untere Grenze des neuen Intervalls?
Der Hersteller möchte weiterhin das Intervall [814.43; 855.57] verwenden (siehe c.). Jedoch soll dafür die Wahrscheinlichkeit, dass die angebene Füllmenge enthalten ist, auf \( \mathbf{9 2} \% \) gesteigert werden (siehe d.). Die Varianz müsste vom Hersteller auf wie viel \( \mathbf{g}^{2} \) gesenkt werden?