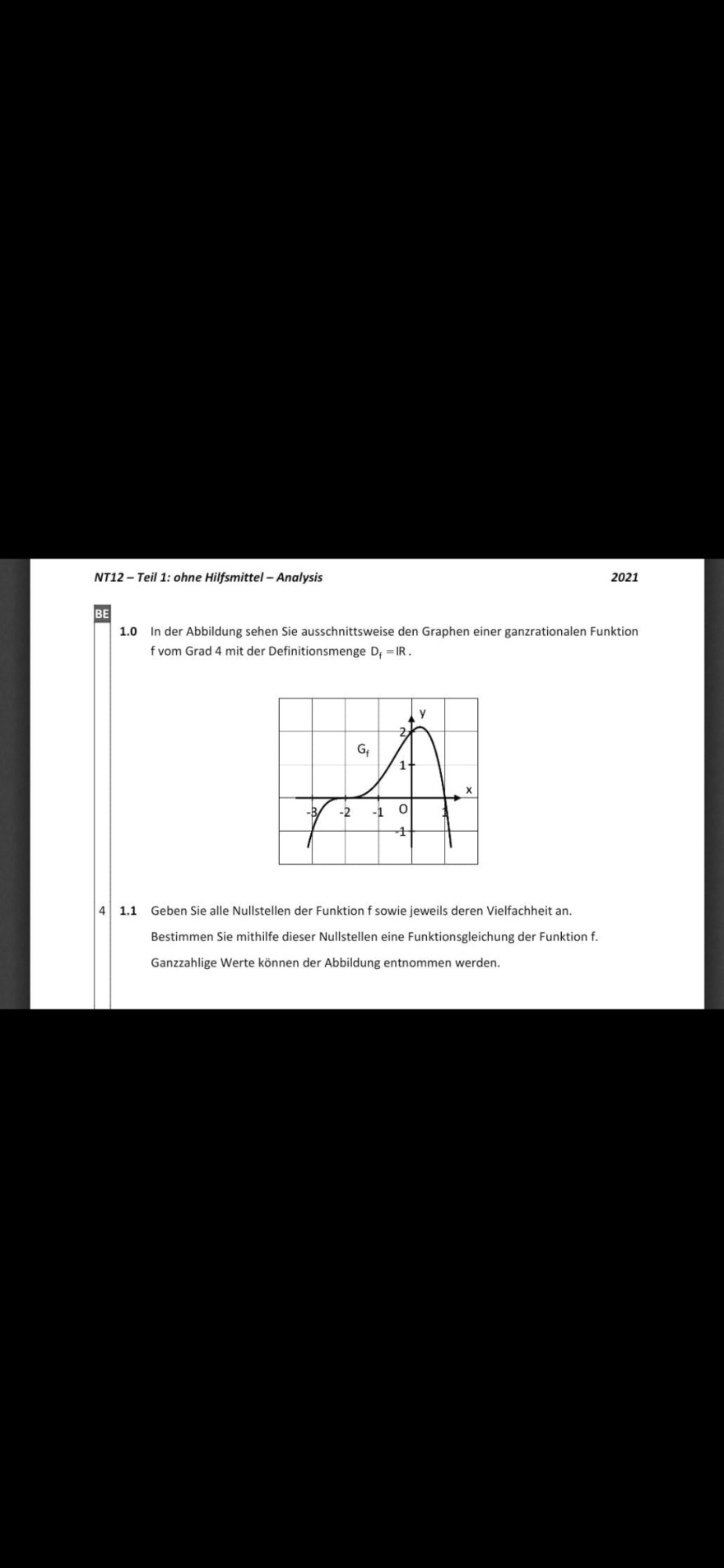
1.0 In der Abbildung sehen Sie ausschnittsweise den Graphen einer ganzrationalen Funktion \( f \) vom Grad 4 mit der Definitionsmenge \( D_{f}=I R \).
4 1.1 Geben Sie alle Nullstellen der Funktion \( f \) sowie jeweils deren Vielfachheit an.
Bestimmen Sie mithilfe dieser Nullstellen eine Funktionsgleichung der Funktion \( f \).
Ganzzahlige Werte können der Abbildung entnommen werden.
Meine Lösung wäre jetzt
a * ( x - 1) * (x + 2)3
Aber wie komme ich auf den Leitkoeffizienten a?
Oder bin ich komplett falsch?