Aufgabe:

Text erkannt:
Gegeben sei die Drehung \( \varphi: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}:\left(\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right) \mapsto \frac{1}{9}\left(\begin{array}{ccc}1 & -4 & 8 \\ -8 & -4 & -1 \\ 4 & -7 & -4\end{array}\right)\left(\begin{array}{l}x_{1} \\ x_{2} \\ x_{3}\end{array}\right) \).
(a) Bestimmen Sie den Kosinus des Drehwinkels \( \alpha \) : \( \quad \cos (\alpha)=-\frac{8}{9} \).
(b) Betrachten Sie nun die verschobene Drehung \( \mu: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}: x \mapsto \varphi(x)+b \) mit \( b=\left(\begin{array}{c}0 \\ -3 \\ -3\end{array}\right) \).
Bestimmen Sie die Drehachse \( R: \quad R=\left\{\left.\left(\begin{array}{c}\frac{3}{2} \\ -3 \\ 0\end{array}\right)+\lambda\left(\begin{array}{c}\frac{3}{2} \\ -1 \\ 1\end{array}\right) \right\rvert\, \lambda \in \mathbb{R}\right\} \)
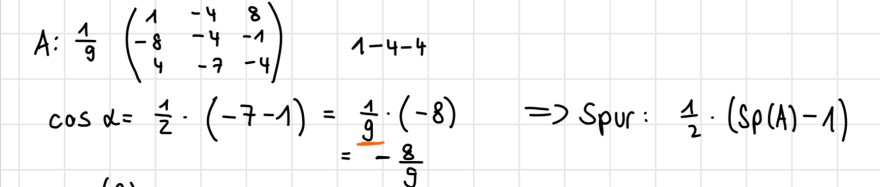
Text erkannt:
\( \begin{aligned} A: \frac{1}{9}\left(\begin{array}{rrr}1 & -4 & 8 \\ -8 & -4 & -1 \\ 4 & -7 & -4\end{array}\right) & 1-4-4 \\ \cos \alpha=\frac{1}{2} \cdot(-7-1) & =\frac{1}{9} \cdot(-8) \quad \Rightarrow \operatorname{Spur}: \frac{1}{2} \cdot(\operatorname{Sp}(A)-1) \\ & =\frac{-8}{9}\end{aligned} \)
Problem/Ansatz:
Hallo,
folgende Aufgabe habe ich leider falsch. Beim Drehwinkel bin ich davon ausgegangen, dass die Formel aus Bild 2 verwendet werden soll und verstehe nicht, wie man darauf kommt.
Bei der Drehachse habe ich auf der Haupdiagonalen -9 jeweils abgezogen und das Lgs =0 gesetzt, bekomme aber andere Werte raus. Ist mein Vorgehen falsch?