Vielen Dank!
Nachdem ich didses LGS aufgestellt habe und für t=0,1 setzte, erhalte ich die gesuchte Matrix A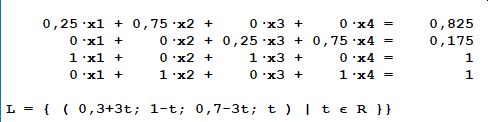
Text erkannt:
\( \begin{array}{l}\mathrm{L}=\{(0,3+3 \mathrm{t} ; 1-\mathrm{t} ; 0,7-3 \mathrm{t} ; \mathrm{t}) \mid \mathrm{t} \in \mathrm{R}\}\} \\\end{array} \)
\begin{pmatrix} 0,6 & 0,9 \\ 0,4 & 0,1 \end{pmatrix}