Aufgabe:

Text erkannt:
c) Skipisten, die mit dem Schwierigkeitsgrad „mittel“ gekennzeichnet sind, haben ein Gefälle von höchstens \( 40 \% \).
- Berechnen Sie den zum Gefälle \( 40 \% \) gehörigen Neigungswinkel.
Der Start einer \( 850 \mathrm{~m} \) langen Abfahrt mit annähernd konstantem Gefälle liegt auf einer Seehöhe von \( 1240 \mathrm{~m} \), das Ziel auf \( 912 \mathrm{~m} \).
- Überprüfen Sie nachweislich, ob diese Abfahrt "mittel“ sein kann.
Problem/Ansatz:
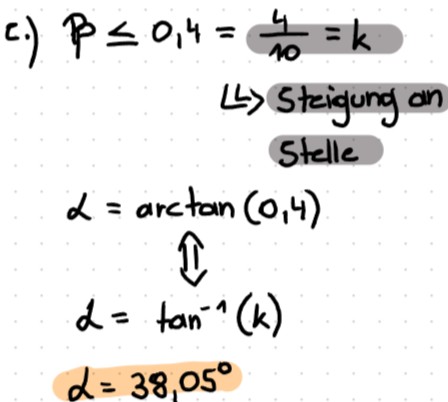
Text erkannt:
c.)
\( \begin{array}{l} \beta \leq 0,4=\frac{4}{10}=k \\ \longleftrightarrow \text { Steigung an } \\ \text { Stelle } \end{array} \)
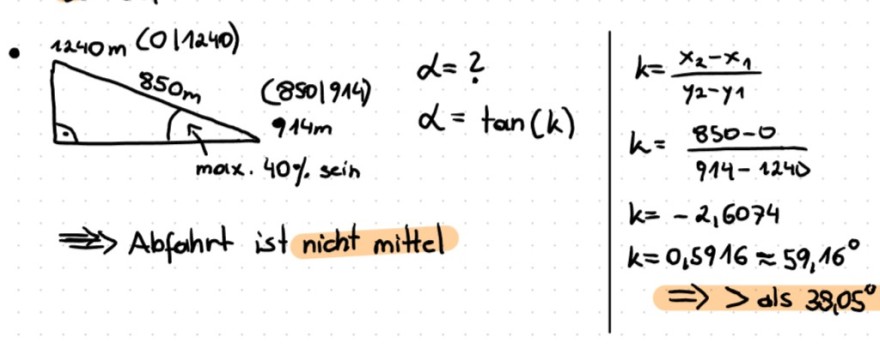
Ich würde gerne wissen, was an meinem Ergebnis falsch ist, weil im laut der Lösung bei dem ersten Punkt für Alpha = 21,80° rauskommen soll und bei der Überprüfung, ob die Abfahrt mittel ist 22,70°?