Integralrechnung, y Achse

Question

Aufgabe:
Die Parabel f(x) = - 1/4x^2 + 2x schließt mit der y-Achse und der Tangente im Kurvenpunkt P(6/3) ein Flächenstück vollständig ein. Legen Sie eine Skizze an und berechnen Sie den Flächeninhalt.

Comments

Dann fang mal mit der Skizze an. Was stellst Du fest? Welches Integral muss berechnet werden?

---

Aha. Und was ist Deine Frage dazu?

---

Lösung mit Geogebra

Answer 1

Hallo,

\(f(x)=\frac{-1}{4}x^2+2x\\ f'(x)=-\frac{1}{2}x+2\\ P(6\mid3)\\ f'(6)=-1\\\)

Wende für die Tangentengleichung die Punktsteigungsform an. Mögl. Schreibweise

\(t(x)=f'(x_0)\cdot (x-x_0)+f(x_0)\)

[spoiler]

\(t(x)=-1\cdot (x-6)+3=-x+6+3=-x+9\)

[/spoiler]

Berechne dann das Integral zwischen t und g von 0 bis 6.

[spoiler]

\( \begin{array}{l}\int \limits_{0}^{6} t(x)-f(x)=\int \limits_{0}^{6} \frac{1}{4 }x^2-3x+9 \\[15 pt] =\left[\frac{1}{12} x^{3}-\frac{3}{2}x^2+9x\right]_{0}^{6} \\[15 pt] =\frac{1}{12} \cdot 6^{3}-\frac{3}{2} \cdot 6^{2}+9 \cdot 6=18\end{array} \)

[/spoiler]

Gruß, Silvia

Answer 2

Tangentengleichung t(x):

t(x) = (x-6)*f '(6) +3

Berechne den Berührpunkt f(x) = t(x)

Integriere t(x) - f(x) von 0 bis zur Berührstelle.

https://www.wolframalpha.com/input?i=-0.25x%5E2%2B2x%2C+-x%2B9+from+0+to+10

Answer 3

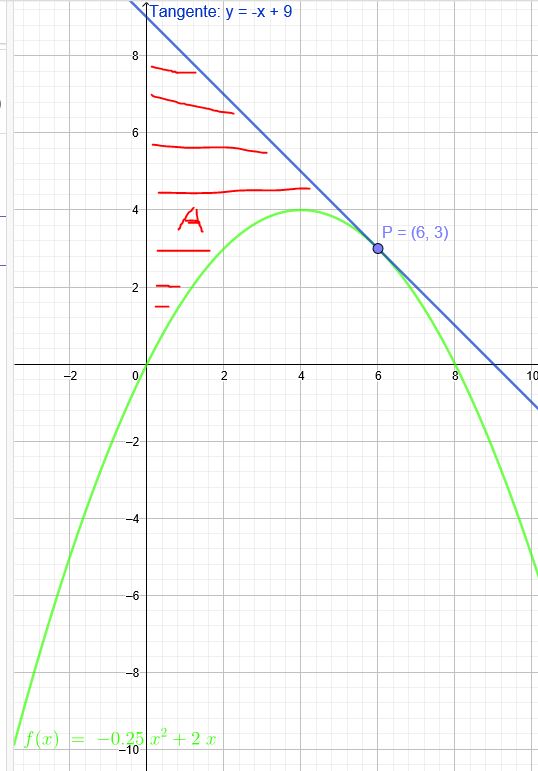
Die Parabel \(f(x) = - 0,25x^2 + 2x\) schließt mit der y-Achse und der Tangente im Kurvenpunkt \(P(6|3) \)ein Flächenstück vollständig ein. Legen Sie eine Skizze an und berechnen Sie den Flächeninhalt.

Tangente:

\(f'(x) = - 0,5x + 2\)

\(f'(6) = -3 + 2=-1\)

\( \frac{y-3}{x-6}=-1 \) →    \( y=-x+9 \)

Flächenstück unter der Tangente:

\( A_1= \int\limits_{0}^{6}(-x+9)dx=[-0,5x^2+9x]_{0}^{6} = [-0,5 \cdot 36+54]-0=36\)

Flächenstück unter der Parabel:

\(A_2= \int\limits_{0}^{6} (- \frac{1}{4}x^2 + 2x)dx=[-\frac{1}{12}x^3+x^2]_{0}^{6}=[-\frac{1}{12} \cdot 6^3+36   ] -0=18 \)

Gesuchtes Flächenstück:

\(A=A_1-A_2=36-18=18\)

Das gesuchte Flächenstück ist  \(A=18FE\) groß.