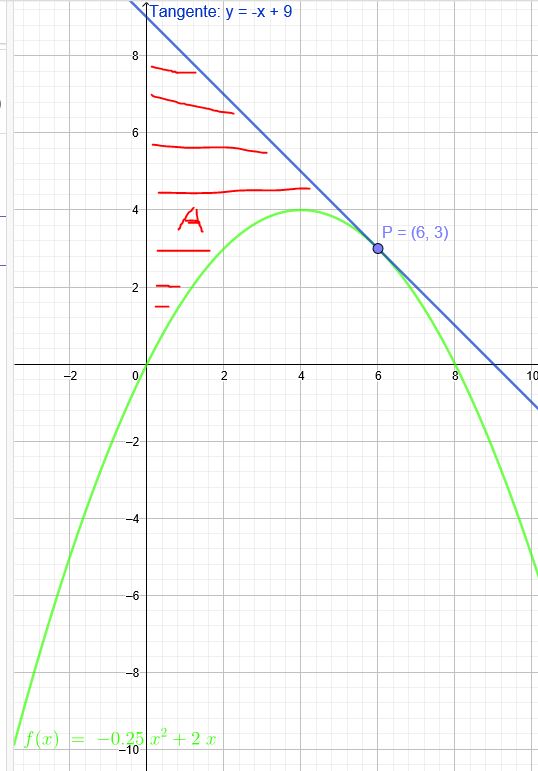
Die Parabel f(x)=−0,25x2+2x schließt mit der y-Achse und der Tangente im Kurvenpunkt P(6∣3)ein Flächenstück vollständig ein. Legen Sie eine Skizze an und berechnen Sie den Flächeninhalt.
Tangente:
f′(x)=−0,5x+2
f′(6)=−3+2=−1
x−6y−3=−1 → y=−x+9
Flächenstück unter der Tangente:
A1=0∫6(−x+9)dx=[−0,5x2+9x]06=[−0,5⋅36+54]−0=36
Flächenstück unter der Parabel:
A2=0∫6(−41x2+2x)dx=[−121x3+x2]06=[−121⋅63+36]−0=18
Gesuchtes Flächenstück:
A=A1−A2=36−18=18
Das gesuchte Flächenstück ist A=18FE groß.