Aufgabe: Noch eine Frage zu der Anderen Seite der vollständigen Induktion. In der oberen Zeile steht zwei mal
2 n+1 bei bei der unteren Zeile steht das nur noch einmal. Mit den Potenzen hat das ja nichts zutun. Was für ein verfahren kommt da zur Anwendung?
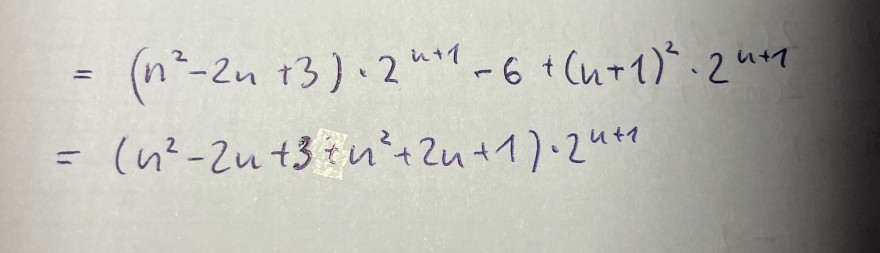
Text erkannt:
\( \begin{array}{l}=\left(n^{2}-2 n+3\right) \cdot 2^{n+1}-6+(n+1)^{2} \cdot 2^{n+1} \\ =\left(n^{2}-2 n+3+n^{2}+2 n+1\right) \cdot 2^{n+1}\end{array} \)
Problem/Ansatz: Hallo Leute, kann mir bitte noch jemand sagen wieso es auf der zweiten Zeile nur noch eine 2n+1 gibt? Danke für die Mühe
mfg