Aufgabe:
Hallo
Problem/Ansatz:

Text erkannt:
2. Aufgabe: Volumenintegrale
a) Berechnen Sie das Volumen des Körpers in \( \mathbb{R}^{3} \), der im ersten Oktant (d.h. \( x \geq 0 \), \( y \geq 0, z \geq 0) \) enthalten ist und durch die Fläche \( z=4-x^{2}-y \) eingeschränkt ist.

Text erkannt:
\( \begin{array}{l}2 a) \\ \int \limits_{0}^{2} \int \limits_{0}^{-x^{2}+4} 4-x^{2}-y d y d x \\ =\underbrace{\int \limits_{0}^{2} \int \limits_{0}^{-x^{2}+4} 4 d y d x}_{1 .}-\underbrace{\iint_{0}^{2} \int \limits_{0}^{-x^{2}+4} x^{2} d y d x}_{2}-\underbrace{\int \limits_{0}^{2} \int \limits_{0}^{-x^{2}+4} y d y d x}_{3 .} \\ \text { 1.: } \int \limits_{0}^{2}-4 x^{2}+16 d x=\left[-\frac{4}{3} x^{3}\right]_{0}^{2}+16[x]_{0}^{2} \\ =-\frac{4}{3} \cdot 8+32=32-\frac{32}{3} \\ =\frac{96}{3}-\frac{32}{3}=\frac{64}{3} \\ 2.8+\int^{2} x^{4}-4 x^{2} d x=\frac{1}{5}\left[x^{5}\right]_{0}^{2}-\frac{4}{3}\left[x^{3}\right]_{0}^{2} \\\end{array} \)
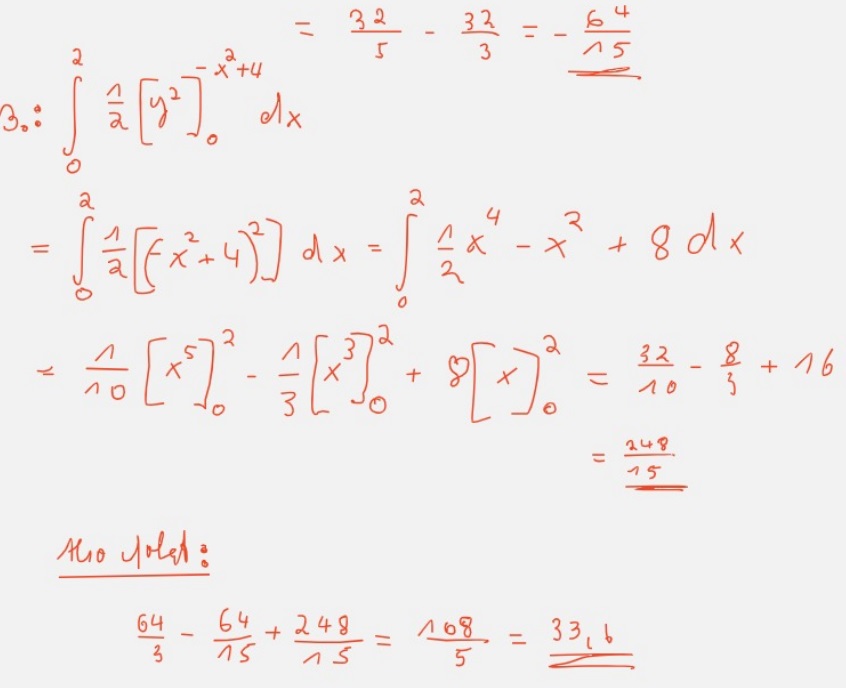
Text erkannt:
\( \begin{array}{l} 3 .: \int \limits_{0}^{2} \frac{1}{2}\left[y^{2}\right]_{0}^{-x^{2}+4} d x \\ =\int \limits_{0}^{2} \frac{1}{2}\left[\left(x^{2}+4\right)^{2}\right] d x=\int \limits_{0}^{2} \frac{1}{2} x^{4}-x^{2}+8 d x \\ =\frac{1}{10}\left[x^{5}\right]_{0}^{2}-\frac{1}{3}\left[x^{3}\right]_{0}^{2}+8[x]_{0}^{2}=\frac{32}{10}-\frac{8}{3}+16 \\ =\frac{248}{15} \end{array} \)
tho folat:
\( \frac{64}{3}-\frac{64}{15}+\frac{248}{15}=\frac{168}{5}=33,6 \)
Kann jemand sagen ob der Rechenweg richtig ist, also die Integrationsgrenzen. Bin da gerade iwie raus.
Danke im Voraus