Grenzwert der n-ten Wurzel einer Subtraktion mit Werten die n als Exponenten haben.

Question

Aufgabe:

Text erkannt:

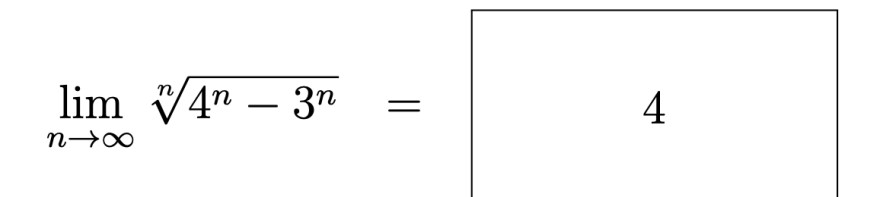
\( \lim \limits_{n \rightarrow \infty} \sqrt[n]{4^{n}-3^{n}}= \)

Problem/Ansatz:

Hallo Zusammen, wie kommt man auf das Ergebnis? ChatGPT meint, dass 4^n der dominierende Faktor ist und denkt sich die 3^n komplett und daraus folgt 4. Stimmt das überhaupt? Darf man das? Wenn ja wieso? Wenn nicht wie soll man hier vorgehen?

Answer 1

Für n -> oo kann man 3^n vernachlässigen.

(4^n)^(1/n) = 4^1 = 4

oder so:

4^n ausklammern: [√(4^n*(1- (3/4)^n)]^(1/n)

Teilwurzel ziehen: 4*[√1-(3/4)^n]^(1/n) = 4*1 = 4 

(3/4)^n geht gg. Null.

Comments

ahhhhhh okay macht sinn, vielen dank