Aufgabe: Logarithmus interpretieren
…
Problem/Ansatz:
Skate-Park. Nachstehende Abbildung zeigt das (vertikale) Profil eines Hinderniselements in einem Skate-Park. Es liegt im gewählten Koordinatensystem symmetrisch bezüglich der y-Achse und besteht aus den Graphen zweier Funktionen f und g sowie einer 4m langen waagrechten Strecke. Der nach rechts fallende Teil des Profils lässt sich beschreiben durch die Funktion f (es ist nur die funktion f gegeben und die steht beim anderen Bild in geogebra)
(a) Geben Sie eine Gleichung der Funktion g an. (Habe ich schon gemacht mit geogebra, also g(x)=f(-x)
(b) Zeichnen Sie den Winkel a = 180° + arctan(f'(2)) in obiger Abbildung ein. (habe ich versucht, es kommt 135 grad raus, aber wo soll ich das einzeichnen?
(c) Interpretieren Sie mit den aussagekräftigsten Begriffen im Sachzusammenhang jene Stelle Xm. die
durch folgende Gleichung definiert ist. [1P]
f'(Xm) = (f(8) - f(2))/ (8-2)
(d) Die Fahrbahn auf der Rampe ist 3m breit. Zur Berechnung der Fahrbahnfläche ist die Länge des
Rampenprofils mit der Breite zu multiplizieren.
Berechnen Sie die Fahrbahnfläche der Rampe. [1P]
(e) Begründen Sie mithilfe der Differentialrechnung, dass der Graph von f nach rechts fallend ist. 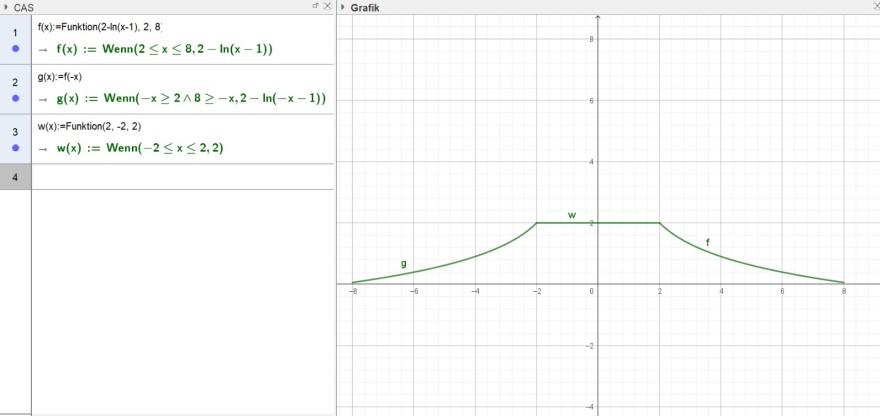
Text erkannt:
CAS
Grafik
\( f(x):= \) Funktion(2-In \( (x-1), 2,8 \);
\( \rightarrow \mathrm{f}(\mathrm{x}):=\operatorname{Wenn}(2 \leq \mathrm{x} \leq 8,2-\ln (\mathrm{x}-1)) \)
\( g(x):=f(-x) \)
\( \rightarrow \mathrm{g}(\mathrm{x}):=\operatorname{Wenn}(-\mathrm{x} \geq 2 \wedge 8 \geq-\mathrm{x}, 2-\ln (-\mathrm{x}-1)) \)
\( w(x):= \) Funktion \( (2,-2,2) \)
\( \rightarrow \mathrm{w}(\mathrm{x}):=\operatorname{Wenn}(-2 \leq \mathrm{x} \leq 2,2) \)