Reihen und Konvergenz

Question

Aufgabe:

a) Erstmal war zu zeigen:

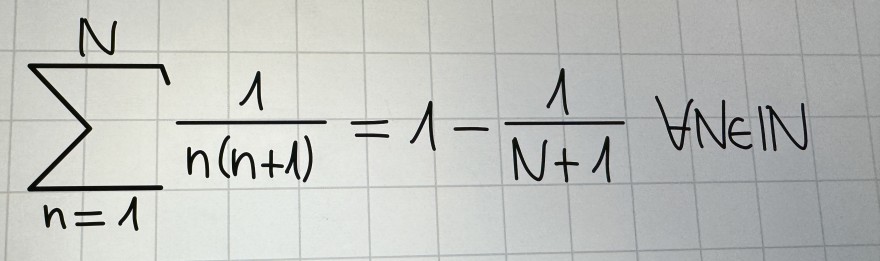
Text erkannt:

\( \sum \limits_{n=1}^{N} \frac{1}{n(n+1)}=1-\frac{1}{N+1} \forall N \in \mathbb{N} \)

Das ist ja leicht, einfach mit vollständiger Induktion.

Mein Problem ist aber bei der darauffolgenden Aufgabe. Ich soll nun mittels dem Resültat zeigen, das die harmonische Reihe mit Exponent 2, also

Σ 1/n^2, konvergiert. Allgemein ist die Konvergenz dieser Reihe ja bekannt, nur ich verstehe nicht, was damit gemeint ist, das ich es mittels dem Resültat von a) zeigen soll.

Answer 1

Wenn \(\sum \limits_{n=1}^{N} \frac{1}{n(n+1)} \) konvergiert, konvergiert erst recht die Summe mit den kleineren Summanden \(\sum \limits_{n=1}^{N} \frac{1}{(n+1)(n+1)} \). Mit einer Indexverschiebung wird daraus \(\sum \limits_{n=2}^{N} \frac{1}{n\cdot n} \). Die Hinzunahme des Summanden \( \frac{1}{1\cdot 1} \) (damit das Ganze wieder bei n=1 starten kann) ändert auch nichts an der Konvergenz.

Comments

Danke sehr! :)