Wie berechne ich die Höhe h in einem rechtwinkligen Dreieck ABC mit der Hypotenuse \(c=15\) cm und den beiden Katheten \(a= 9\)cm und \(b= 12\)cm.
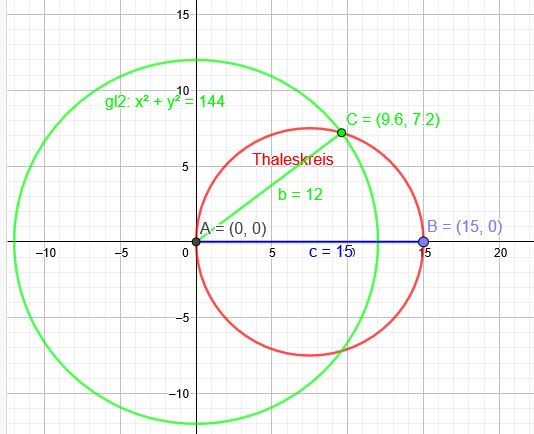
Thaleskreis über der Strecke A nach B:
\((x-7,5)^2+y^2=7,5^2\)
Kreis um A mit \(r=12\):
\(x^2+y^2=144\) schneidet \((x-7,5)^2+y^2=7,5^2\) in C:
\((x-7,5)^2+144-x^2=7,5^2\)
\(x=9,6\) einsetzen in \(9,6^2+y^2=144\): \(y=7,2\) Negativwert entfällt.
Das Dreieck hat eine Höhe von \(7,2\) cm