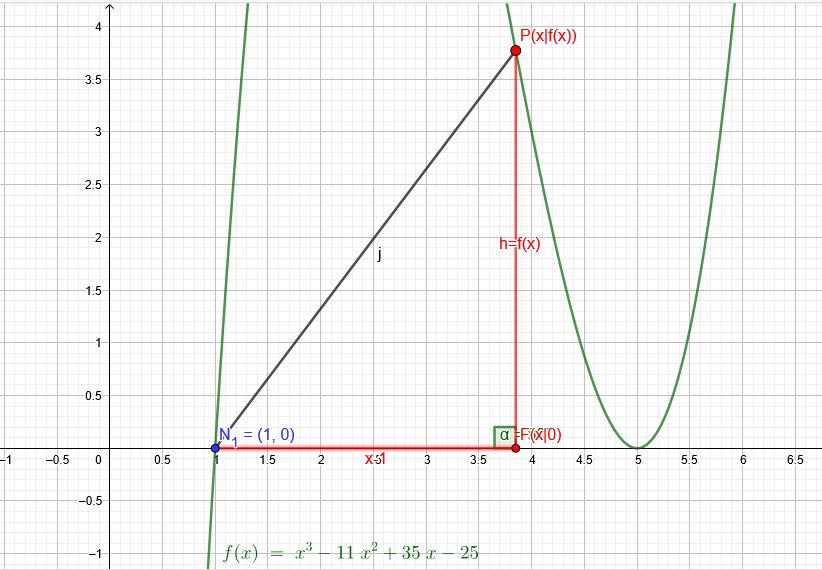
Zielfunktion:
\(A(x)=\frac{1}{2} \cdot (x-1)\cdot f(x) \) für \(x ∈[1;5]\) soll maximal werden.
Nebenbedingung:
\(f(x)=x^3-11x^2+35x-25\)
\(A(x)=\frac{1}{2} \cdot (x-1)\cdot (x^3-11x^2+35x-25) \)
\(A'(x)\) bestimmen und \(A'(x)=0\) setzen.
Dann den maximalen Flächeninhalt bestimmen.