Funktions Schar Schnittpunkt

Question

Aufgabe:

Text erkannt:

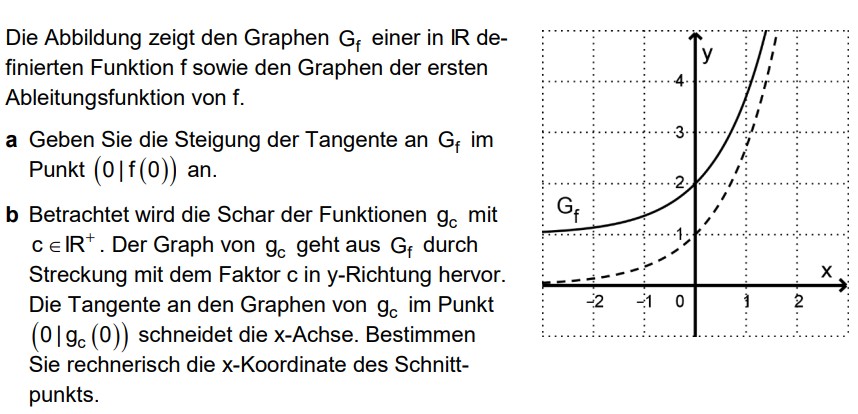
Die Abbildung zeigt den Graphen \( G_{f} \) einer in IR definierten Funktion \( f \) sowie den Graphen der ersten Ableitungsfunktion von \( \mathrm{f} \).
a Geben Sie die Steigung der Tangente an \( \mathrm{G}_{\mathrm{f}} \) im Punkt (0|f(0)) an.
b Betrachtet wird die Schar der Funktionen \( g_{c} \) mit \( c \in \mathbb{R}^{+} \). Der Graph von \( g_{c} \) geht aus \( G_{f} \) durch Streckung mit dem Faktor \( \mathrm{c} \) in y-Richtung hervor. Die Tangente an den Graphen von \( g_{c} \) im Punkt \( \left(0 / g_{c}(0)\right) \) schneidet die \( x \)-Achse. Bestimmen Sie rechnerisch die \( x \)-Koordinate des Schnittpunkts.

Nur b) unklar:

Ich habe zunächst die Tangentengleichung aufgestellt:

y= gc(0)' *x +gc(0)

Ich will diese vereinfachen, weiß aber nicht wie.

Weil ich will die Gleichung danach mit 0 gleichsetzen um den Schnittpunkt zu erhalten.

Ich verstehe aus dem Text nicht, wie die Tangente vereinfacht werden könnte.

Answer 1

Es ist \( g_c(x) =cf(x) \). Folglich ist \( g'_c(x) =cf'(x) \). Teil a) hast du ja.

Comments

Achso Streckung in y-Richtung bedeutet dass der Faktor mit der Funktion multipliziert wird also -> c*f(x) . Gut, das verstehe ich.

Aber mich verunsichert dass bei der Ableitung nur f'(x) abgeleitet wird und nicht c.

Könnte ich das mit dem Beispiel begründen?:

Wenn ich zb 2*(2x+1) ableite wird ja auch nur die Funktion in der Klammer abgeleitet und mit dem Faktor multipliziert. Und deswegen f'(x) mal den Faktor c.

---

Das ist die Faktorregel bei Ableitungen. Nicht verwechseln mit der Produktregel. Aber genau so ist es.