Gleichung des Polynoms 2. Grades aufstellen

Question

Aufgabe:

Wie lautet die Gleichung des Polynoms 2. Grades, das bei P(1,5/1) eine waagerechte Tangente hat und bei y= 2,5 die y Achse schneidet?

Ich habe leider keinen Ansatz wie ich die Aufgabe lösen soll

Answer 1

Scheitelpunktform ist

        $f(x) = a(x-1,5)^2 + 1$

Punkt $(0|2,5)$ einsetzen und Gleichung lösen.

Answer 2

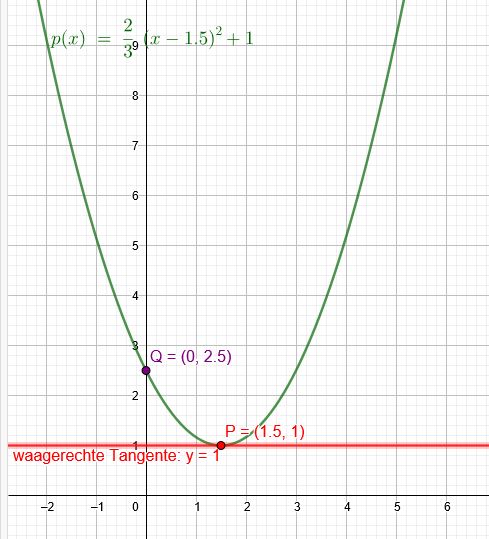
Wie lautet die Gleichung des Polynoms 2. Grades, das bei $P(1,5|\red{1})$ eine waagerechte Tangente hat und bei $y= 2,5$ die y Achse schneidet?

Ich verschiebe den Graphen um $\red{1}$ Einheit nach unten→ $P´(1,5|0)$ Dort ist nun eine doppelte Nullstelle.

$f(x)=a \cdot (x-1,5)^2$

bei $y= 2,5$ die y Achse schneidet: $Q(0|2,5)$  →$Q´(\green{0}|\red{1,5})$

$f(\green{0})=a \cdot (\green{0}-1,5)^2=2,25a$

$2,25a=\red{1,5}$    →$a=\frac{2}{3}$

$f(x)=\frac{2}{3} \cdot (x-1,5)^2$

$\red{1}$ Einheit nach oben:

$p(x)=\frac{2}{3} \cdot (x-1,5)^2+\red{1}$

Comments

Molietius locutus imagine adiecta, causa finita. :)

Answer 3

f(x) = ax²+bx+c

f '(x) = 2ax +b

f(1,5) = 1

f '(1,5) = 0

f(0) = 2,5

2,25a+1,5b+c= 1

3a+b= 0 -> b = -3a

c= 2,5

2,25a-4,5a+2,5 = 1

-2,25a = -1,5

a= 2/3

b= -2

f(x) = 2/3*x²-2x+2,5

Comments

Dankeschön, jetzt habe ich es verstanden

---

Und die Antwort von Oswald hast du nicht verstanden?

---

Vlt. hätte er noch dazusagen sollen, dass P der Scheitel ist.

---

Erst nachdem ich die Aufgabe jetzt gelöst habe, ist mit der Zusammenhang klar geworden mit der Scheitelpunktform