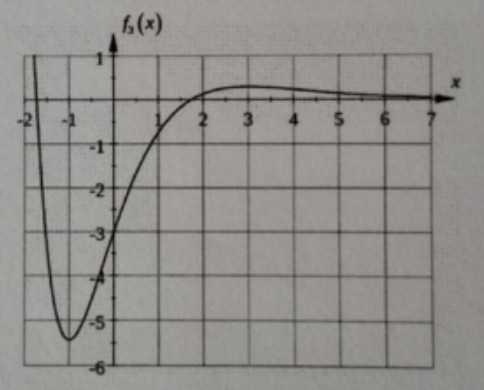
c) Es wird nun die Funktion \( f_{3} \) der oben genannten Schar betrachtet, d. h., es gilt \( f_{3}(x)=\left(x^{2}-3\right) \cdot e^{-x}, x \in \mathbb{R} . \) Der Graph der Funktion \( f_{3} \) wird am Ende der Aufgabenstellung dargestellt.
(1) Es sei \( u \) eine beliebige reelle Zahl. Begründen Sie mit Hilfe partieller Integration:
\( \int \limits_{0}^{\infty} f_{3}(x) d x=\left(-u^{2}-2 u+1\right) \cdot e^{-v}-1 \).
(2) Berechnen Sie mit Hilfe von c) (1) den Inhalt der Fläche, die von dem Graphen der Funktion \( f_{3} \) und der x-Achse im III. und IV. Quadranten eingeschlossen wird.