Untersuchen Sie auf Konvergenz und bestimmen Sie gegebenenfalls den Grenzwert oder alle Häufungspunkte

Question

Aufgabe:

Untersuchen Sie auf Konvergenz und bestimmen Sie gegebenenfalls den Grenzwert
oder alle Häufungspunkte:

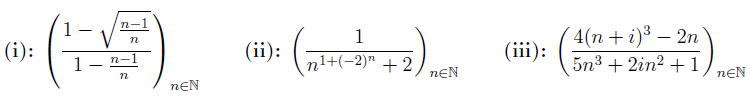
Problem/Ansatz:

Ich bin bei i) lediglich soweit gekommen durch einsetzen von mehreren Werten für n, dass ich weiß die Folge läuft gegen 0,5. Danach habe dass hier versucht:

$$ \left | a_{n}-a \right |=\left | a_{n}-0,5 \right | = \left | \frac{1-\sqrt{\frac{n-1}{n}}}{1-\frac{n-1}{n}}-0,5 \right | \leq \frac{1-\sqrt{\frac{N-1}{N}}}{1-\frac{N-1}{N}}< \varepsilon $$

Bin mir dann aber nicht sicher wie nach N umstelle. Kann mir dabei jemand helfen?

Comments

Diese Aufgaben sollen in der Regel nicht mit Hilfe der Definition der Konvergenz gelöst werden, sondern mit Hilfe von Umformungen, Abschätzungen und vor allem Grenzwertsätzen. Bei der ersten Aufgabe bietet sich zum Beispiel eine Erweiterung gdes Bruchs mit \((1+\sqrt{...})\) an (oder einer anderweitigen Verwendung einer binomischen Formel)

Answer 1

Hallo

i)mit n erweitern, dann oben n*√(1-1/n ) Für kleine 1/n 1. Taylor √(1-1/n)=1+1/(2n)

ii gerade und ungerade n ansehen.

iii

durch n^3 kürzen

Gruß lull