Lineare Algebra Beweis

Question

Aufgabe: Gegeben ist diese lineare Abbildung (Das sie limear ist, wurd schon bewiesen)

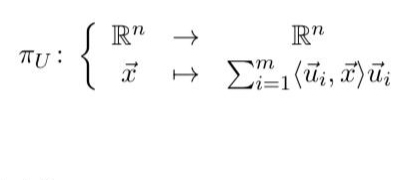
Text erkannt:

\( \pi_{U}:\left\{\begin{array}{rcc}\mathbb{R}^{n} & \rightarrow & \mathbb{R}^{n} \\ \vec{x} & \mapsto & \sum \limits_{i=1}^{m}\left\langle\vec{u}_{i}, \vec{x}\right\rangle \vec{u}_{i}\end{array}\right. \)

Dann sei U noch ein linearer Unterraum mit Dimension m (endlichdimensional) mit einer Orthonormalbasis u1,…,u_m.

Zu zeigen war, das im(π_U) = U ist.

Meine Idee: (Es ist noch kein Beweis!)

Also ich hatte die Idee, das wenn u ein beliebiges Element von U ist, hat es ja aufgrund der Orthonormalbasis u1,…,u_m eine Darstellung als Linearkombination, da ja u1,…,u_m wegen der Basiseigenschaft erzeugend und linear unabhängig sind und damit U = span(u1,…,u_m) gilt. Also z.B. u = a1*u1 + … + a_m*u_m, wobei a1,..,a_m die darstellenden reelen Skalare sind. Nun ja wenn u auch ein Element von dem Bild sein soll, dann muss es ja ein Urbild x aus R^n geben, sodass π_U(x) = u ist, da es ja sonst nicht im Bild liegen dürfte. D.h. dann gilt auch

u = π(x) = <u1,x>*u1 + … + <u_m,x>*u_m, wobei die eindeutig darstellenden Skalarprodukte hier die reelen Skalare sind. Hiermit würde ja u auch in U liegen, da U ja gerade die Menge aller Linearkombinationen der Basisvektoren u1,…,u_m ist und auch umgekehrt.

Ist die Idee richtig und könnte man es so in der Art als Beweis formulieren?

Answer 1

Hallo

Du solltest doch einfacher einfach mal die Bilder der Basisvektoren ansehen. wenn man etwa u1 abbildet fallen alle Summanden <u1,un> n≠1 weg , dann sieh erst das Bild von x als Linearkombination  der ui

das greift ja deine Idee mit auf

lul

Comments

Kann man das x denn als Linearkombination von den Basisvektoren von U darstellen, denn das ist ja im R^n, was ja nicht zwingend dem Unterraum U entsprechen muss?

Oder ist die Idee hier, die Basis u1,…,u_m zu einer Basis u1,…,u_n zu erweitern und dann x als Linearkombination darzustellen, da ja dann R^n = span(u1,…,u_n) gilt

---

hallo

wenn du IM(U) bildest, hast du doch nur x∈U abzubilden?

lul

---

ich mach das mal gleich, ich verstehe glaube ich was Du meinst.

---

Ich hab jetzh zwei Inklusionen gemacht. Ist das als Beweis so richtig?

Erste Inklusion:

Text erkannt:

Sei \( u \in U \). Es giet \( u=\sum \limits_{k=1}^{m} \lambda_{k} u_{k} \) mit \( \lambda_{k} \in \mathbb{R} \)
Damit folgt:
\( \begin{array}{l} u=\sum \limits_{k=1}^{m} \lambda_{k} u_{k}=\sum \limits_{k=1}^{m} \lambda_{k} \pi\left(u_{k}\right) \\ =\pi\left(\sum \limits_{k=1}^{m} \lambda_{k} u_{k}\right)=\pi(u) \in B_{i} l d(\pi) \end{array} \)

Linearität

Zweitw Inklusion:

Text erkannt:

,\( _{1,} O^{11} \)
Sei \( u \in \forall \operatorname{Bild}(\pi), d \cdot h x \in \mathbb{R}^{n}: \pi(x)=u \). Da U die Menge aller Linearkombinationen der vehtoren \( U_{1}, . . u_{m} \) ist, also \( U=\left\{\lambda_{1} u_{1}+\ldots+\lambda_{m} u_{m} \mid \lambda_{i} \in \mathbb{R}\right\}=\left(\operatorname{in}\left(u_{1} \ldots u_{m}\right)\right. \) ist also \( u=\pi(x)=\left\langle u_{1}, x\right\rangle u_{1}+\ldots+\left\langle u_{m}, x\right\rangle u_{n} \) mit testen Skalaren \( \left\langle u_{i}, x\right\rangle \in \mathbb{R} \) cuich aus \( U \)

---

Hallo

du musst wohl explizit hinschreiben warum π(ui)=ui

lul

---

Es gilt ja <u_i, u_j> = 0 für i ≠ j und

<u_i, u_j> = 1 für i = j (Stichwort: Kronecker Delta) da u1,…,u_m ein Orthonormalsystem ist.

Darauf folgt dann:

π(u_i) = <u_1, u_i> * u1 + … + <u_m, u_i> * u_m = <u_i, u_i> * u_i = u_i

da <u_i, u_i> = 1 ist und der Rest wegfällt.

Ist also hiermit der Beweis korrekt?

---

Hallo

soweit ich sehe ja

lul

---

Dankeschön! :)