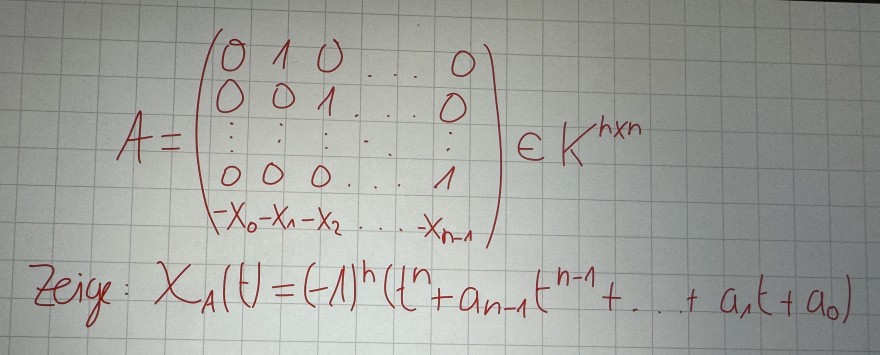
Text erkannt:
\( \begin{array}{l} A=\left(\begin{array}{ccccc}0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ -x_{0}-x_{1}-x_{2} & \cdots & -x_{n-1}\end{array}\right) \in K^{n \times n} \\ \text { Zeige: } X_{A}(t)=(-1)^{n}\left(t^{n}+a_{n-1}\left(t^{n-1}+\ldots+a_{1} t+a_{0}\right)\right.\end{array} \)
Hi, diese Matrix aus dem Format (n x n) ist gegeben und ich soll zeigen, das das Polynom da, das charakteristische Polynom ist.
Meine Idee war es, zuerst einmal die Eigenschaften eines charakteristischen Polynoms zu nutzten. Hierbei haben wir eine n x n Matrix und damit wissen wir das Polynom hat den Grad n.
Also hat es die allgemeine Form
XA(t) = c_n * t^n + c_(n-1) * t^(n-1) + … + c_1 * t + c_0, wobei c_n = (-1)^n, c_(n-1) = -(-1)^n * Spur(A) und c_0 = det(A) ist. (Aus der VL)
Ich berechnete diese und kam auf:
c_n = (-1)^n, c_(n-1) = (-1)^n * a_(n-1) und c_0 = (-1)^n * a_0. Mit Einsetzten fogt ja:
XA(t) = (-1)^n * t^n + (-1)^n a_(n-1) * t^(n-1) + … + c_1 * t + (-1)^n a_0. Das ist ja alles bis auf den Term c_1 * t, das was ich zeigen soll. Jedoch ist mein Problem bei diesem Term, hierbei muss ja c_1 = (-1)^n * a_1 sein und allgmein für 0 < i < n-1, c_i = (-1)^n * a_i. Ich weiss aber nicht wie ich es zeigen soll. Kann mir einer helfen?