Aufgabe:
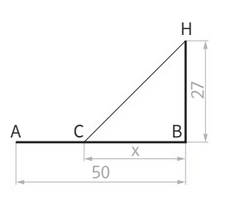 Auf der Straße von A nach B (A B = 50 km) hat B mit 27km den kürzesten
Auf der Straße von A nach B (A B = 50 km) hat B mit 27km den kürzesten
Abstand zum Haus H. Von A aus soll eine Wasserleitung zum Haus H
verlegt werden. Die Kosten für die Verlegung betragen längs der
Straße AB 120€ pro Laufmeter und im Gelände neben der Straße 165€
pro Laufmeter. Wo muss die Abzweigung C gewählt werden, damit die
Gesamtkosten möglichst klein werden? Wie hoch sind die minimalen
Gesamtkosten?
Problem/Ansatz:
… Könntet ihr mir bitte beim lösen dieser Aufgabe helfen...? Ich hätte zunächst f(x)= (50-x)·120+\( \sqrt{x^2+27^2} \) ·165 aufgestellt.. Die Ableitung davon wäre ja f'(x)=165x/(x2+272), rauskommen sollen ca. 36(km), ich erhalte aber stets x=72·\( \sqrt{57} \) /19 ≈28,16(km). Was mache ich falsch?
Herzlichen Dank vorab...