Fehler: Dateityp „pdf“ ist nicht erlaubt.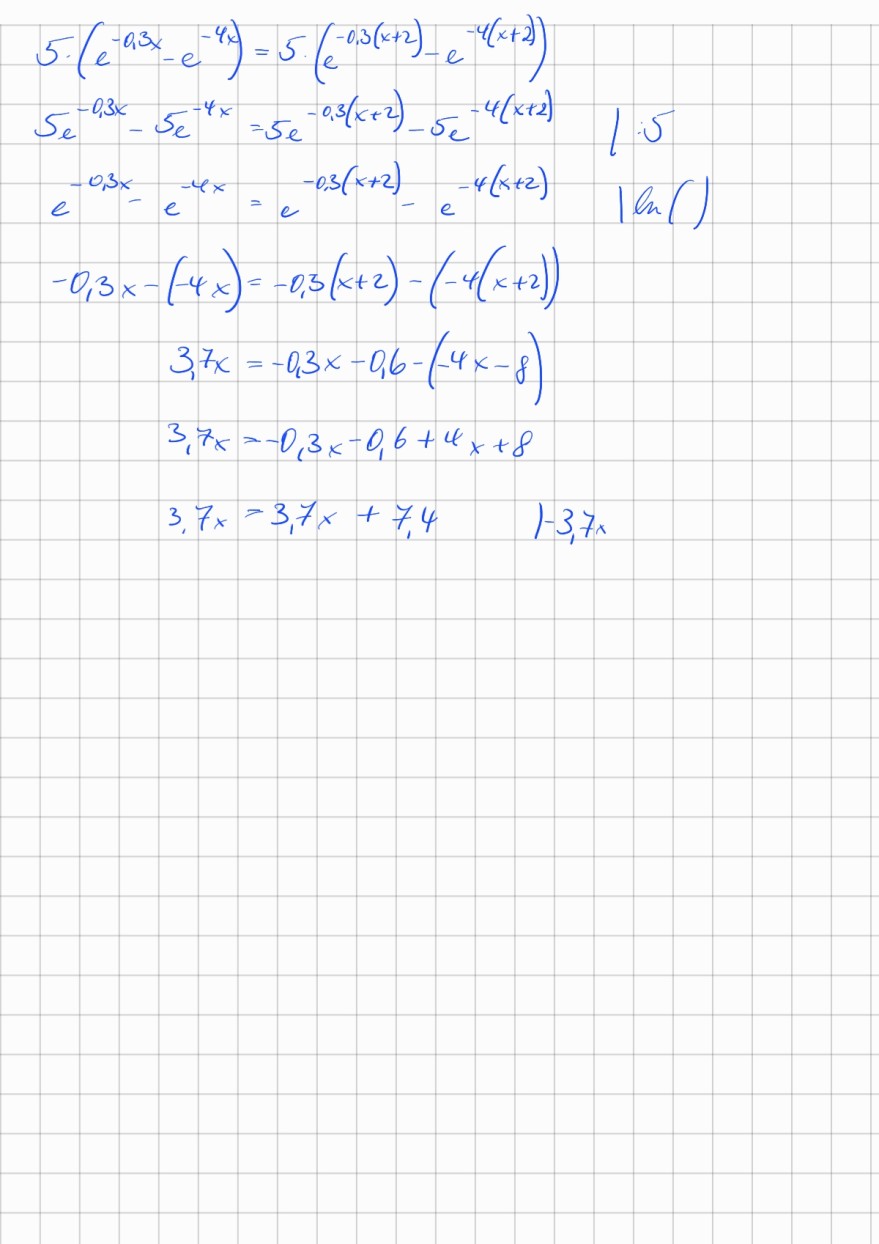
Text erkannt:
\( \begin{aligned} 5 \cdot\left(e^{-0,3 x}-e^{-4 x}\right) & =5 \cdot\left(e^{-0,3(x+2)}-e^{-4(x+2)}\right) \\ 5 e^{-0,3 x}-5 e^{-4 x} & =5 e^{-0,3(x+2)}-5 e^{-4(x+2)} \quad \mid: 5 \\ e^{-0,3 x}-e^{-4 x} & =e^{-0,3(x+2)}-e^{-4(x+2)} \quad \mid \ln () \\ -0,3 x-(-4 x) & =-0,3(x+2)-(-4(x+2)) \\ 3,7 x & =-0,3 x-0,6-(-4 x-8) \\ 3,7 x & =-0,3 x-0,6+4 x+8 \\ 3,7 x & =3,7 x+7,4 \quad \mid-3,7 x\end{aligned} \)
Iwas hab ich falsch gemacht...