Berechnung der Koordinaten der tangenten

Question

Aufgabe:
Berechnen Sie die Koordinaten der Punkte, in denen der Graph der Funktion f(x)=(x² −4x+3)∗(x+2) (x∈R) Tangenten besitzt, die parallel zur Geraden g mit der Gleichung y= −x + 6  (x∈R) verlaufen.

Problem/Ansatz:

Ich komme einfach nicht auf die Lösung... jedoch weiß ich das die Tangente die gleiche Steigung wie g hat als 0?

Comments

die parallel zur Geraden g mit der Gleichung = − + 6 (R) verlaufen.

Das ist keine Geradengleichung. Wie lautet sie wirklich?

g(x)= y= .....

Wie lautet f(x) korrekt?

---

Weder 'Funktion f()=(² −4+3)∗(+2)(∈R)' noch 'Geraden g mit der Gleichung = − + 6 (R)' ergibt Sinn.

---

Oh entschuldige bitte y=-x+6

---

Und f(x) = ???

---

Scheinbar wurde die Funktion nicht richtig kopiert

---

Jetzt sollte es alles richtig dastehen, entschuldigt bitte

---

Tippe sie ab und stelle sie ein!

---

Steht jetzt alles richtig da...
f(x)=(x² −4x+3)∗(x+2)

g(x)=y=−x + 6

Answer 1

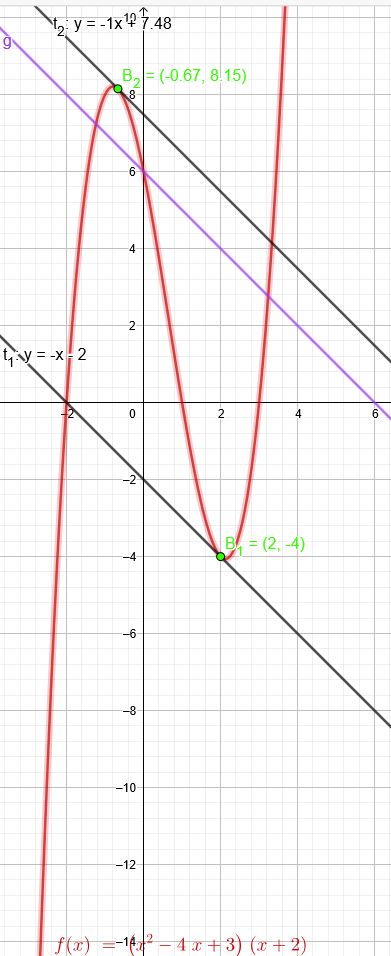
Berechnen Sie die Koordinaten der Punkte, in denen der Graph der Funktion $f(x)=(x^2 −4x+3)∗(x+2)$ mit $(x∈R)$ Tangenten besitzt, die parallel zur Geraden g mit der Gleichung $y= −x + 6$ mit $(x∈R)$ verlaufen.

$f(x)=(x^2 −4x+3) \cdot (x+2)$

Produktregel  $(F_1\cdot F_2)'=F'_1\cdot F_2+F_1 \cdot F'_2)$

$f'(x)=(2x −4)\cdot(x+2)+(x^2 −4x+3)\cdot1$

Die Gerade $y= \red{−1}x + 6$  hat die Steigung $\red{−1}$

$\red{−1}=(2x −4)\cdot(x+2)+(x^2 −4x+3)$

$2x^2+4x-4x-8+x^2 −4x+3= \red{−1}$

$3x^2−4x=4|:3$

$x^2−\frac{4}{3}x=\frac{4}{3}$

$x^2−\frac{4}{3}x+(\frac{2}{3})^2=\frac{4}{3}+(\frac{2}{3})^2$

$(x−\frac{2}{3})^2=\frac{12}{9}+\frac{4}{9}=\frac{16}{9} |±\sqrt{~~}$

1.)

$x−\frac{2}{3}=\frac{4}{3}$

$x_1=2$     $f(2)=(2^2 −4 \cdot 2+3) \cdot (2+2)=...$

2.)

$x−\frac{2}{3}=-\frac{4}{3}$

$x_2=-\frac{2}{3}$     $f(-\frac{2}{3})=...$

Comments

Wenn du in dem Thread denkst, dass es nicht schlimmer kommen kann...

---

Vielen Dank, so habe ich es jetzt auch aufgeschrieben...

---

Und was hast du verstanden...?

---

Wie ich die x-Koordinaten ausrechne... das habe ich auch schon bei Abakus gelernt, schlussendlich kann ich die y-Koordinaten auch simple ausrechnen lassen mittels CAS etc. allerdings war für mich Abakus Lösung nicht richtig da diese über dem Graphen der Funktion f(x) lag, Moliets hat die gleiche Lösung wie ich und sein Punkt liegt auf dem Graphen ist faktisch also richtig...

Zudem muss man sagen das ich zu keiner Zeit gesagt habe das ich lernen möchte wie so etwas funktioniert sondern ich wollte die Lösung, @Moliets hat das direkt gemacht und das auch noch mit Rechen weg ist für mich also die beste Lösung auf meinen Thread.

liebe Grüße

---

Schlechte Idee, wenn man nur die Lösung möchte, aber nichts lernen möchte. Muss ja jeder für sich selbst entscheiden, wie weit man damit kommt.

Wenn du allerdings vorher schon eine Lösung und Rechenweg hast, liefere sie doch direkt mit. Dann müssen sich andere nicht die Mühe machen, dir alles von Grund auf zu erklären. Man kann dann gezielt nach Fehlern oder den Schwierigkeiten suchen.

Answer 2

Die Gerade hat die Steigung -1. Berechne also die Stellen mit $f'(x) =-1$.

Comments

Ich danke dir erst ein mal für deine Antwort... allerdings habe ich wirklich null Ahnung wie ich das rechne :(

---

Bilde die erste Ableitung!

Bevor du dich mit der Produktregel rumquälst, solltest du (x² −4x+3)∗(x+2) ausmultiplizieren, dann kannst du direkt ableiten.

Was erhältst du beim Ausmultiplizieren von (x² −4x+3)∗(x+2)?

---

Erste Ableitung ist F´(x)=3*x2-4x-5

Answer 3

Die Gerade y= −x + 6 hat den Anstieg -1.

Wenn der Graph deiner Funktion Tangenten haben soll die zu dieser Gerade parallel sind, dann müssen diese Tangenten AUCH den Anstieg -1 haben.

Hast du die erste Ableitung schon gebildet?

Comments

Erste Ableitung: F´(x)=3*x²-4x-5

---

Ja. Und die muss -1 werden. Löse also 3x²-4x-5=-1

---

Lieber Abakus... ist {2;-0.667} richtig?

---

Ist die Tangente -x-2?

---

Lieber Abakus... ist {2;-0.667} richtig?

Die Lösung x=2  ist richtig.

Die Lösung x=-0,667 ist falsch. Richtig ist hier x=-2/3.

Ist die Tangente -x-2?

Wen interessiert es? Das ist nicht gefragt. Gefragt waren PUNKTE auf dem Graphen von f.

Die Punkte sind (2|...) und (-2/3|...).

Um die y-Koordinate zu berechnen hast du die Funktionsgleichung
f(x)=(x² −4x+3)∗(x+2)

---

Das stimmt, mein Fehler

(2;-4) und (-2/3;8,148) Richtig?

---

Du hast mit 8,148 schon wieder einen Näherungswert gebracht, der vom tatsächlichen Ergebnis abweicht. Kannst du ((-2/3)²-4·(-2)/3 +3)·(-2/3  +2) wirklich nicht exakt ausrechnen?

Das sind nämlich exakt 236/27.

Das mit dem Stützunterricht war doch keine schlechte Anregung.

---

8,148 habe ich mit dem CAS Taschenrechner im Grafikmenu bestimmt...

Mathe ist:

1. Nicht das Fach mit meiner Priorität
2. Schreibe ich sonst gute Noten in Mathe also ist mir das relativ egal
3. Ist Abi in ca 4 Wochen ist also zu spät

Answer 4

f(x) = (x²-4x+3)(x+2) = x³+2x²-4x²-8x+3x+6 = x³-2x²-5x+6

f '(x)= 3x²-4x-5

Es muss gelten:

f '(x) = g'(x) = -1

3x²-4x-5= -1

3x²-4x-4 = 0

x²- 4/3*x-4/3 = 0

pq-Formel:

x1/2= 2/3+-√(4/9+4/3) = 2/3+- 4/3

x1= 2

x2= -2/3

t1(x) = (x-2)*f '(2) + f(2)

Die Tangenten müssen dieselbe Steigung haben wie die Gerade, hier: m= -1 (Faktor vor x)

t1(x) = ...

t2(x) = (x+2/3)*f '(-2/3) + f(-2/3)

t2(x) = ...

Comments

Danke das du mir gleich noch deine Rechnung aufschreibst... ich bin in Mathe scheinbar echt massivst unbegabt... was sind die Lösungen? Vlt. begreife ich es dann

---

Du musst t1 und t2 nur noch ausrechnen und zusammenfassen.

Berechne also f und f ' für x= 2 bzw. x= -2/3.

Das schaffst du doch, oder?

---

Nicht wirklich nein, hatte vorhin meine Lehrerin gefragt... die meinte ich hätte in den Mathe Stützunterricht gehen sollen, kann nicht wirklich verstehen wieso ich für sowas in den Stützunterricht sollte... bin eher der meinung sowas hätten wir im Unterricht machen sollen... haben wir aber nicht, also nein ich kann es nicht.

---

@ggT

Arbeite an deiner Lesekompetenz.

t2(x) = (x+2/3)*f '(-2/3) + f(-2/3)

war ÜBERHAUPT NICHT gefragt.

Für Punkte, deren x-Koordinate du vorgerechnet hast, ist noch die y-Koordinate zu berechnen. Fertig.

---

Wo liegen die Punkte denn jetzt schluss endlich?

---

@abakus:

Diese Mehrarbeit kann nicht schaden. Tangenten aufstellen muss man können.

So muss auch der TS eine Eigenleistung erbringen.

---

Es mag sein das ich das aufstellen können muss allerdings kann ich das auch noch später lernen, jetzt muss ich erstmal meine Aufgabe Abgeben, die zeit drängt also

---

Es war gut gemeint. Ich dachte, das hatte ihr schon. Sorry.

---

So muss auch der TS eine Eigenleistung erbringen.

Dann einfach mal weniger vorrechnen. ;)