Integration durch Partialbruchzerlegung einfache reelle Nullstellen

Question

Aufgabe:

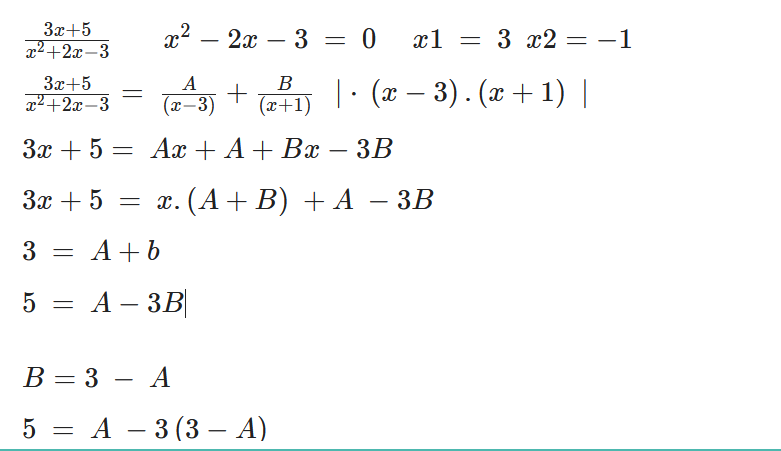
Text erkannt:

\( \begin{array}{l}\frac{3 x+5}{x^{2}+2 x-3} \quad x^{2}-2 x-3=0 \quad x 1=3 x 2=-1 \\ \frac{3 x+5}{x^{2}+2 x-3}=\frac{A}{(x-3)}+\frac{B}{(x+1)}|\cdot(x-3) \cdot(x+1)| \\ 3 x+5=A x+A+B x-3 B \\ 3 x+5=x \cdot(A+B)+A-3 B \\ 3=A+b \\ 5=A-3 B \\ B=3-A \\ 5=A-3(3-A)\end{array} \)

Text erkannt:

\( A=\frac{7}{2} \quad B=-\frac{1}{2} \)

Hey Leute, könnt ihr bitte schauen, wo ich mich verrechnet habe, Lösungsbuch sagte \( =A=2, B=1 \)

Problem/Ansatz:

…

Comments

Lautet der Nenner \(x^2+2x-3\) oder \(x^2-2x-3\) ?

---

Zur Kontrolle ein anderer Weg:

https://www.integralrechner.de/

Answer 1

Schon die Faktorzerlegung ist vom Vorzeichen falsch

x^2 + 2·x - 3 = (x - 1)·(x + 3)

Damit kommst du auf

(3·x + 5)/(x^2 + 2·x - 3) = 1/(x + 3) + 2/(x - 1)