Gleichungssystem mit Inverse lösen

Question

Aufgabe:

Gleichungssystem mithilfe der inversen Matrix lösen:

Problem/Ansatz:

ich habe das Problem, dass ich bei 3 und 2,5 nicht weiß, wie ich die 3 mit einer 0 ersetzt bekomme.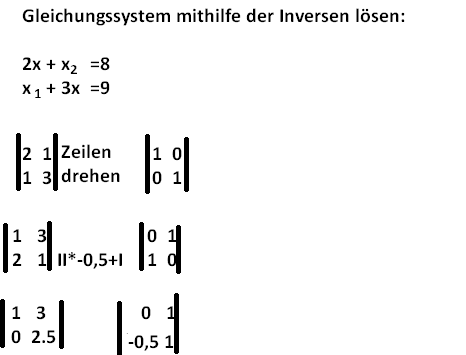

Text erkannt:

Gleichungssystem mithilfe der Inversen lösen:
\( \begin{array}{l} 2 x+x_{2}=8 \\ x_{1}+3 x=9 \end{array} \)
\( \begin{array}{l} \left|\begin{array}{ll|l} 2 & 1 \\ 1 & 3 \end{array}\right| \text { Zeilen }\left|\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right| \\ \left.\left|\begin{array}{ll} 1 & 3 \\ 2 & 1 \end{array} I^{*-0,5+1}\right| \begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array} \right\rvert\, \\ \left|\begin{array}{ll} 1 & 3 \\ 0 & 2.5 \end{array}\right| \quad\left|\begin{array}{cc} 0 & 1 \\ -0,5 & 1 \end{array}\right| \\ \end{array} \)

Comments

Nutze doch diese Formel für die Inverse $$A^{-1} = \frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}$$

---

ich habe das Problem, dass ich bei 3 und 2,5 nicht weiß, wie ich die 3 mit einer 0 ersetzt bekomme.

Teile die 2.te Zeile durch 2,5, dann steht da eine 1.

Dann ziehe die 2. Zeile drei mal von der ersten ab.

---

Muss es nicht 3x1 lauten?

Answer 1

Bilde das kleinste gemeinsame Vielfache, oder wenn es gar nicht geht, die eine Zeile mal 3 und die andere mal 2,5 und dann subtrahieren. Eine Division würde ich immer vermeiden, wenn sie nicht ganzzahlig aufgeht.

Answer 2

$$A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \newline A^{-1} = \frac{1}{ad-bc}\cdot \begin{pmatrix} d & -b \\ -c & a \end{pmatrix} \newline \text{Bei dir also wie folgt:} \newline A = \begin{pmatrix} 2 & 1 \\ 1 & 3 \end{pmatrix} \newline A^{-1} = \frac{1}{2 \cdot 3 - 1 \cdot 1}\cdot \begin{pmatrix} 3 & -1 \\ -1 & 2 \end{pmatrix} \newline A^{-1} = \frac{1}{5}\cdot \begin{pmatrix} 3 & -1 \\ -1 & 2 \end{pmatrix} = \begin{pmatrix} 3/5 & -1/5 \\ -1/5 & 2/5 \end{pmatrix} = \begin{pmatrix} 0.6 & -0.2 \\ -0.2 & 0.4 \end{pmatrix}$$