Aufgabe:
Ich möchte keine Lösung oder Rechenweg, vielmehr habe ich eine Verständnis Frage zu den Regeln des Gauß verfahren.
Problem/Ansatz:
Text erkannt:
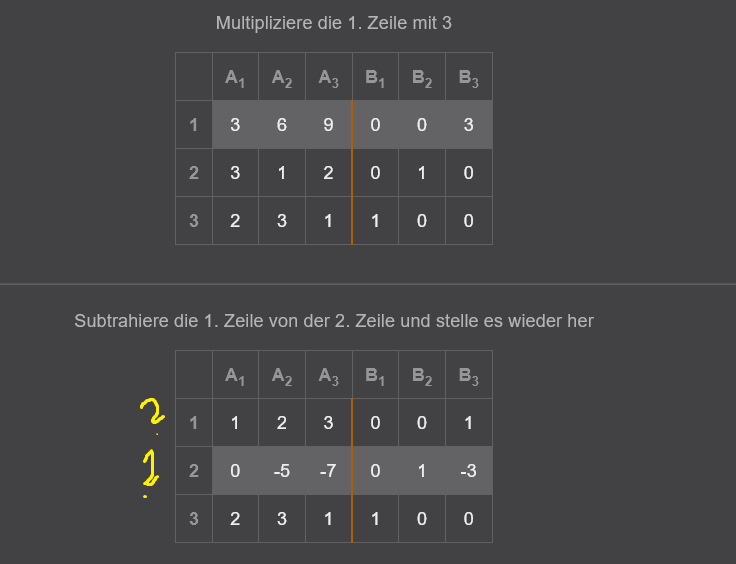
Multipliziere die 1. Zeile mit 3
\begin{tabular}{|c|c|c|c|c|c|c|}
\hline & \( \mathrm{A}_{1} \) & \( \mathrm{~A}_{2} \) & \( \mathrm{~A}_{3} \) & \( \mathrm{~B}_{1} \) & \( \mathrm{~B}_{2} \) & \( \mathrm{~B}_{3} \) \\
\hline 1 & 3 & 6 & 9 & 0 & 0 & 3 \\
\hline 2 & 3 & 1 & 2 & 0 & 1 & 0 \\
\hline 3 & 2 & 3 & 1 & 1 & 0 & 0 \\
\hline
\end{tabular}
Subtrahiere die 1. Zeile von der 2. Zeile und stelle es wieder her
\begin{tabular}{|c|c|c|c|c|c|c|}
\hline & \( A_{1} \) & \( \mathrm{~A}_{2} \) & \( \mathrm{~A}_{3} \) & \( B_{1} \) & \( B_{2} \) & \( \mathbf{B}_{3} \) \\
\hline 1 & 1 & 2 & 3 & 0 & 0 & 1 \\
\hline 2 & 0 & -5 & -7 & 0 & 1 & -3 \\
\hline 3 & 2 & 3 & 1 & 1 & 0 & 0 \\
\hline
\end{tabular}
In der Abbildung sieht ihr in Zeile Zwei, dass die erste Zeile von der zweiten Zeile Subtrahiert wird. um eben dort die 0 zu bekommen, gleichzeitig wird einfach auch die 1. Zeile berechnet um 1 und 0 zu haben,das geht doch nicht so? Wenn ich die Zweite Zeile berechne und dort die Operation - durchführe, bleibt die erste Zeile gleich und nur die zweite wird geändert. Seit wann kann man zwei Zeilen mit einem Operator verändern oder liege ich falsch?