Hallo,
hier einige Tipps:
Aufgabe ii:
Substituiere: z= y -x+4 ---->Tipp verworfen
neue Substitution:
z =x-4 und
v=y/z
siehe Lösungsweg:

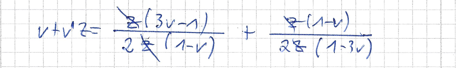
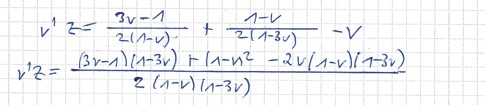

weiterer Weg:
- Lösung der DGL via Trennung der Variablen
- linkes Integral via Partialbruchzerlegung lösen
- Resubstitution der DGL
-AWB in die Lösung einsetzen
iii)Variation der Konstanten
Es gilt allgemein: y' +A(x) y= B(x)
1.homogene DGL berechnen:
y' +A(x) y= 0->Trennung der Variablen
y' -y/(x ln(x))=0
yh=C1 ln(x)
2. Setze C1= C(x)
yp= C(x) ln(x)
yp'= C'(x) *ln(x) +C(x) * (1/x)
3.Setze yp und yp' in die DGL ein:
C'(x) *ln(x) +C(x) * (1/x) - (C(x) ln(x))/(x ln(x)= x^2 ln(x)
dabei muß C(x) herausfallen, wenn Du richtig gerechnet hast,
C'(x) *ln(x) = x^2 ln(x)
C'(x) = x^2
C(x)=x^3/3
4. yp= x^3/3 *ln(x)
5. y= yh+yp
Lösung: y= C1 ln(x) +x^3/3 *ln(x)
dann die AWB noch in die Lösung einsetzen
iv) Substitution : z=y/x
->y=z*x ->y'=z+z'x
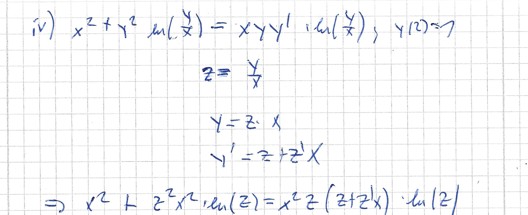
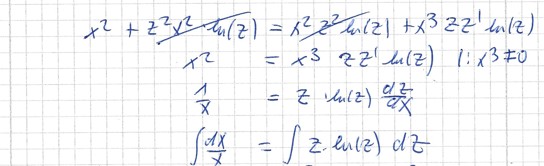

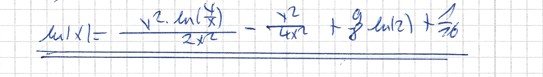
v) Bernoulli-DGL


vi) Exakte DGL


