Aufgabe:
Partielle Ableitung: f(x,y)=1/3x³-x+1/9xy²
Problem/Ansatz:
Mein Prof hat folgende Lösungen für die Ableitung vorgegeben. Damit stelle ich mir die Frage, ob er inkonsistent bei den ersten Ableitungen gearbeitet hat, oder ob ich in irgendeiner weise falsch liege. Hier die folgende Abbildung.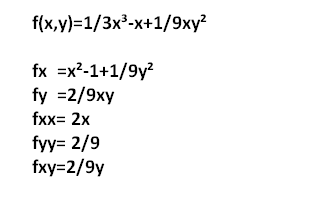
Text erkannt:
\( \begin{array}{l}f(x, y)=1 / 3 x^{3}-x+1 / 9 x y^{2} \\ f x=x^{2}-1+1 / 9 y^{2} \\ f y=2 / 9 x y \\ f x x=2 x \\ f y y=2 / 9 \\ f x y=2 / 9 y\end{array} \)
fx= Stimmt, da x wie eine Zahl behandelt wird und dementsprechend verschwindet.
fy= Ist falsch, da müsste 2/9y stehen. Denn die x verschwindet da es sich hierbei um eine Zahl handelt und aus y² wird y.
fxx= Stimmt, alles verschwindet und x² wird zu 2x
fyy= Stimmt, da muss 2/9 stehen.
Fxy= Stimmt, da müsste 2/9y rauskommen.
Könnt ihr mir bitte sagen, ob meine Gedanken stimmen?