Partielle Ableitung vom Arctan

Question

Ich muss für Physik eine Fehlerfortpflanzungsrechnung machen.

Meine selbst gemessenen Werte sind d und s. Also für diese beiden Werte muss ich in meiner Rechnung eine partielle Ableitung machen.

Die Formeln lauten:

 

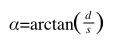
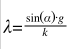
Muss ich jetzt zuerst die Formel für den (Beugungs)Winkel in die, der Wellenlänge Lambda integrieren und dann den großen Term nach d und s partiell ableiten?

Oder leite ich die obere Formel ab und setze dann das kleinste und größte Ergebnis nacheinander in die untere Formel ein?

Wie leite ich überhaupt den arctan ab?

Wäre sehr dankbar über eure Hilfe!!

Answer 1

Hi,
seien $$ a(d,s) = \arctan \left( \frac{d}{s} \right) $$ und
$$ \lambda(d,s) = \sin(a(d,s))\frac{g}{k} $$ die Funktionen für die man die Fehler berechnen muss. Dann gilt
$$ a(d+\Delta d, s + \Delta s) \approx a(d,s) + \frac{\partial}{\partial d} a(d,s)\Delta d + \frac{\partial}{\partial s} a(d,s)\Delta s = $$  $$\frac{d \Delta s - s \Delta d}{d^2 + s^2}  $$

Und für
$$ \lambda(d+\Delta d, s + \Delta s)) \approx \lambda(d,s) + \frac{\partial}{\partial d} \lambda(d,s)\Delta d + \frac{\partial}{\partial s} \lambda\Delta s = $$ gilt
$$  \frac{gs^2\sqrt{\frac{d^2}{s^2}+1}(d \Delta s-s \Delta d)}{k(d^2 +s^2)^2} $$