Hat Graph von f einen Hochpunkt mit positiver x-Koordinate?

Question

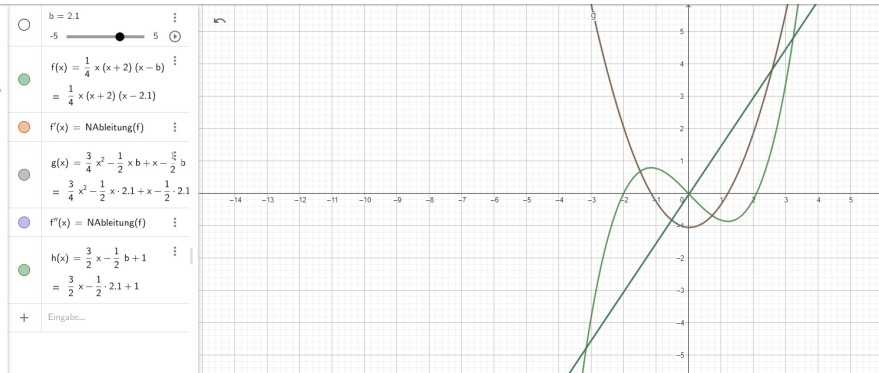
wie kann ich bei der Funktion f begründen, ob

Graph von f  einen Hochpunkt mit positiver x-Koordinate hat?

Für einen festen Wert b, b > 0, ist die Funktion f festgelegt durch:

f(x)= 0.25x(x+2)*(x-b)

Ich habe die Funktion zwei mal abgeleitet.

f'(x)= 3/4x^2-1/2xb+x-1/2b

f''(x)= 3/2x-1/2b+1

Ich müsste beide Funktionen 0 setzen und die Extrema berechnen aber

es kommt ja darauf an, was b ist..

Geht das über diesen Weg oder gibt es einen Weg der besser ist?

Answer 1

Die Funktion hat die Nullstellen -2, 0 und b (mit b>0).

Zwischen -2 und 0 hat die Funktion positive Werte, denn genau 2 der 3 Faktoren x, (x+2) und (x-b) sind dort negativ.

Unter diesen positiven Werten gibt es einen größten.

PS: Was hindert dich daran, die Gleichung

3/4x²-1/2xb+x-1/2b=0 zu lösen und die erhaltenen Lösungen in die zweite Ableitung einzusetzen?

b>0 ist die entscheidende Information zur erfolgreichen Auswertung.

Comments

Was hindert dich daran, die Gleichung

3/4x²-1/2xb+x-1/2b=0 zu lösen und die erhaltenen Lösungen in die zweite Ableitung einzusetzen?

Der Parameter hindert mich.

Ich weiß nicht, wie ich das vereinfachen kann.

Sieht aus wie ABC-Formel aber ich muss dafür -1/2xb+x

zusammenfassen aber keine Ahnung wie.

Weißt du wie?

---

Weißt du wie?

Natürlich. Man klammert x aus.

(3/4)x²-bx/2+x-b/2=0

wird zu

(3/4)x²+(1-b/2)x-b/2=0

Kannst du jetzt a, b und c identifizieren?

---

Ja, dankeschön

a= 3/4

b= 1-b/2

c= -b/2