Für den violetten Winkel bei a) (1):
\(\displaystyle \varphi= \arccos\left(\frac{\overrightarrow{AG} \cdot \overrightarrow{AE}}{\big|\overrightarrow{AG}\big| \cdot \big|\overrightarrow{AE}\big|}\right) = \arccos\left(\frac{\begin{pmatrix} -a\\a\\a \end{pmatrix} \cdot \begin{pmatrix} 0\\0\\a \end{pmatrix}}{\Bigg|\begin{pmatrix} -a\\a\\a \end{pmatrix}\Bigg| \; \cdot \; \Bigg|\begin{pmatrix} 0\\0\\a \end{pmatrix}\Bigg|}=\frac{1}{\sqrt{3}}\right) \)
zum Hinweis von Gast hj2166:
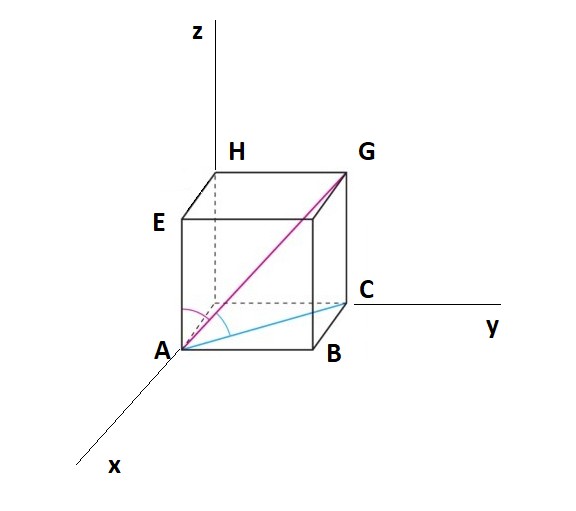
Falls das noch too much sein sollte, betrachte den violetten Winkel im rechtwinkligen Dreieck AGE. Die Länge der Raumdiagonale eines Würfels beträgt das Wurzeldreifache der Kantenlänge (darauf kommt man tatsächlich mit Pythagoras), und im Winkel gilt daher Cosinus = Länge der Ankathete / Länge der Hypotenuse = 1 / \( \sqrt{3} \)
Mein Lieblingstaschenrechner kommt auf einen Winkel von ca. 54,7 Grad, beim blauen Winkel auf arccos(\( \sqrt{2} \) / \( \sqrt{3} \)) ≈ 35,3 Grad. Die beiden Winkel addieren sich auf 90 Grad des Winkels CAE, was man auch in der Abbildung sieht.