Summenzeichen: Seltsame Gleichung

Question

Aufgabe:

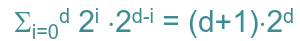
Text erkannt:

\( \sum \limits_{\mathrm{i}=0}^{\mathrm{d}} 2^{\mathrm{i}} \cdot 2^{\mathrm{d}-\mathrm{i}}=(\mathrm{d}+1) \cdot 2^{\mathrm{d}} \)

Problem/Ansatz:

Kann mir jemand erklären, wie diese Gleichheit zustande kommt?

Ich hätte vermutet, dass $$\sum_{i=0}^{d} 2^i \cdot 2^{d-i}=2^d \cdot \sum_{i=0}^{d}2^0=2^d$$

Answer 1

Aloha :)$$\sum\limits_{i=0}^d2^i\cdot 2^{d-i}=\sum\limits_{i=0}^d2^{i+(d-i)}=\sum\limits_{i=0}^d2^d=\underbrace{2^d+2^d+\ldots+2^d}_{(d+1)\text{ Summanden}}=(d+1)\cdot2^d$$

Comments

Besten Dank!