Bestimmen Sie Punkte P(x|f(x) auf dem Graphen so, dass die Tangente in diesen Punkten die x-Achse bei 3,25 schneidet

Question

Aufgabe:

Gegeben ist die Funktion -(x+1)^2+4

Bestimmen Sie Punkte P(x|f(x) auf dem Graphen so, dass die Tangente in diesen Punkten die x-Achse bei 3,25 schneidet

Danke!!!

Comments

https://abiturma.de/mathe-lernen/analysis/tangenten/tangente-durch-fernpunkt

---

Eine Alternative:

der Scheitelpunkt \(S\) der Parabel liegt bei \(S=(-1|\,4)\). Der Brennpunkt \(F\) (hellgrün) liegt bei$$F= \begin{pmatrix} S_x \\ S_y+ \frac{1}{4a}\end{pmatrix}=\begin{pmatrix} -1 \\ 4- \frac{1}{4}\end{pmatrix}\quad a=-1$$\(a\) ist der Faktor vor dem \(x^2\) in der Funktion \(y=-(x+1)^2+4\).

 

Zeichne den Kreis (rot) mit Durchmesser \(|FQ|\). Dieser schneidet die Horizontale (schwarz) durch \(S\) ind \(A\) und \(B\). Die Geraden durch \(AQ\) und \(BQ\) (grün) sind die gesuchten Tangenten an die Parabel.

Die Geraden durch \(FA\) und \(FB\) schneiden die Leitlinie (blau gestrichelt) in \(A'\) und \(B'\) (kleines Bild). Die Schnittpunkte der Vertikalen durch \(A'\) und \(B'\) mit der zugehörigen Tangente sind die gesuchten Punkte \(P(x|\,f(x))\).

Answer 1

Aloha :)

Willkommen in der Mathelounge... \o/

Die Tangente an die Fuktion$$f(x)=-(x+1)^2+4=-x^2-2x+3$$an der Stelle \(x_0\) lautet allgemein:$$t(x)=f(x_0)+f'(x_0)\cdot(x-x_0)$$Wir setzen die Funktion und ihre Ableitung \(f'(x)=-2x-2\) entsprechend ein$$t(x)=\underbrace{(-x_0^2-2x+3)}_{=f(x_0)}+\underbrace{(-2x_0-2)}_{=f'(x_0)}\cdot(x-x_0)$$

Diese Tangente soll die \(x\)-Achse bei \(x=3,25=\frac{13}{4}\) schneiden:$$0\stackrel!=t\left(\frac{13}{4}\right)=\cdots=\frac12(2x_0+1)(x_0-7)$$Es gibt also zwei solche Stellen \((x_0=-\frac12)\) und \((x_0=7)\).

Die zugehörigen Punkte sind \(\pink{P_1(-\frac12\big|\frac{15}{4})}\) und \(\pink{P_2(7\big|-60)}\).

~plot~ -(x+1)^2+4 ; {3,25|0} ; 15/4-(x+1/2) ; {-1/2|15/4} ; -60-16*(x-7) ; {7|-60} ; [[-4|9|-70|10]] ~plot~

Answer 2

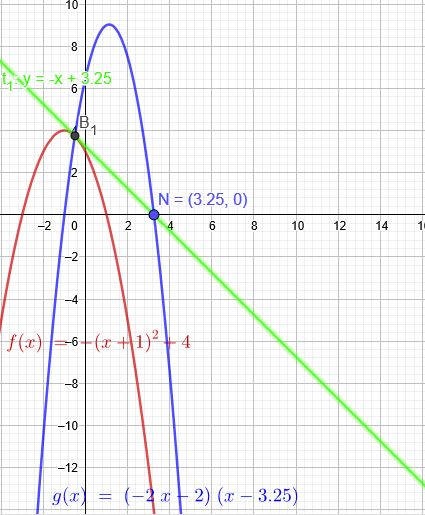
\(f(x)=-(x+1)^2+4\)

\(f´(x)=\orange{-2x-2}\)

Schnittpunkt mit der x-Achse \(N(\red{3,25}|\blue{0})\)

\( \frac{y-\blue{0}}{x-\red{3,25}} =\orange{-2x-2}\)

\( y=(-2x-2)(x-3,25)\)

Diese Parabel schneidet  \(f(x)=-(x+1)^2+4\) in den beiden Berührpunkten.

\(-(x+1)^2+4=(-2x-2)(x-3,25)\)

\(x_1≈-0,5\)  \(f(-0,5)=-(-0,5+1)^2+4=3,75\)

\(x_2=7\)  \(f(7)=-(7+1)^2+4=-60\)