Bestimmen Sie Punkte P(x|f(x) auf dem Graphen so, dass die Tangente in diesen Punkten die x-Achse bei 3,25 schneidet

Question

Aufgabe:

Gegeben ist die Funktion -(x+1)²+4

Bestimmen Sie Punkte P(x|f(x) auf dem Graphen so, dass die Tangente in diesen Punkten die x-Achse bei 3,25 schneidet

Danke!!!

Comments

https://abiturma.de/mathe-lernen/analysis/tangenten/tangente-durch-f…

---

Eine Alternative:

der Scheitelpunkt $S$ der Parabel liegt bei $S=(-1|\,4)$. Der Brennpunkt $F$ (hellgrün) liegt bei$$F= \begin{pmatrix} S_x \\ S_y+ \frac{1}{4a}\end{pmatrix}=\begin{pmatrix} -1 \\ 4- \frac{1}{4}\end{pmatrix}\quad a=-1$$$a$ ist der Faktor vor dem $x^2$ in der Funktion $y=-(x+1)^2+4$.

 

Zeichne den Kreis (rot) mit Durchmesser $|FQ|$. Dieser schneidet die Horizontale (schwarz) durch $S$ ind $A$ und $B$. Die Geraden durch $AQ$ und $BQ$ (grün) sind die gesuchten Tangenten an die Parabel.

Die Geraden durch $FA$ und $FB$ schneiden die Leitlinie (blau gestrichelt) in $A'$ und $B'$ (kleines Bild). Die Schnittpunkte der Vertikalen durch $A'$ und $B'$ mit der zugehörigen Tangente sind die gesuchten Punkte $P(x|\,f(x))$.

Answer 1

Aloha :)

Willkommen in der Mathelounge... \o/

Die Tangente an die Fuktion$$f(x)=-(x+1)^2+4=-x^2-2x+3$$an der Stelle $x_0$ lautet allgemein:$$t(x)=f(x_0)+f'(x_0)\cdot(x-x_0)$$Wir setzen die Funktion und ihre Ableitung $f'(x)=-2x-2$ entsprechend ein$$t(x)=\underbrace{(-x_0^2-2x+3)}_{=f(x_0)}+\underbrace{(-2x_0-2)}_{=f'(x_0)}\cdot(x-x_0)$$

Diese Tangente soll die $x$-Achse bei $x=3,25=\frac{13}{4}$ schneiden:$$0\stackrel!=t\left(\frac{13}{4}\right)=\cdots=\frac12(2x_0+1)(x_0-7)$$Es gibt also zwei solche Stellen $(x_0=-\frac12)$ und $(x_0=7)$.

Die zugehörigen Punkte sind $\pink{P_1(-\frac12\big|\frac{15}{4})}$ und $\pink{P_2(7\big|-60)}$.

Plotlux öffnen

f₁(x) = -(x+1)²+4P(3,25|0)f₂(x) = 15/4-(x+1/2)P(-1/2|15/4)f₃(x) = -60-16·(x-7)P(7|-60)Zoom: x(-4…9) y(-70…10)

Answer 2

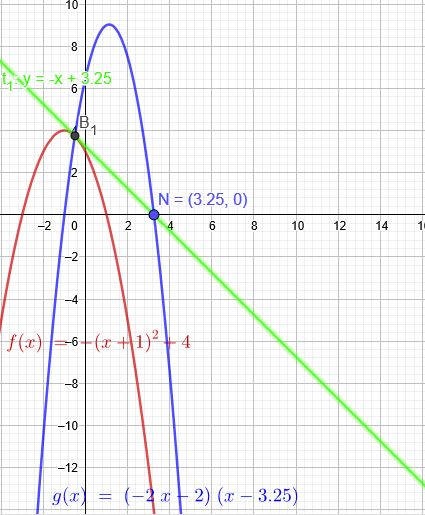
$f(x)=-(x+1)^2+4$

$f´(x)=\orange{-2x-2}$

Schnittpunkt mit der x-Achse $N(\red{3,25}|\blue{0})$

$\frac{y-\blue{0}}{x-\red{3,25}} =\orange{-2x-2}$

$y=(-2x-2)(x-3,25)$

Diese Parabel schneidet  $f(x)=-(x+1)^2+4$ in den beiden Berührpunkten.

$-(x+1)^2+4=(-2x-2)(x-3,25)$

$x_1≈-0,5$  $f(-0,5)=-(-0,5+1)^2+4=3,75$

$x_2=7$  $f(7)=-(7+1)^2+4=-60$