Delfin im Meer holt Luft

Question

Aufgabe:

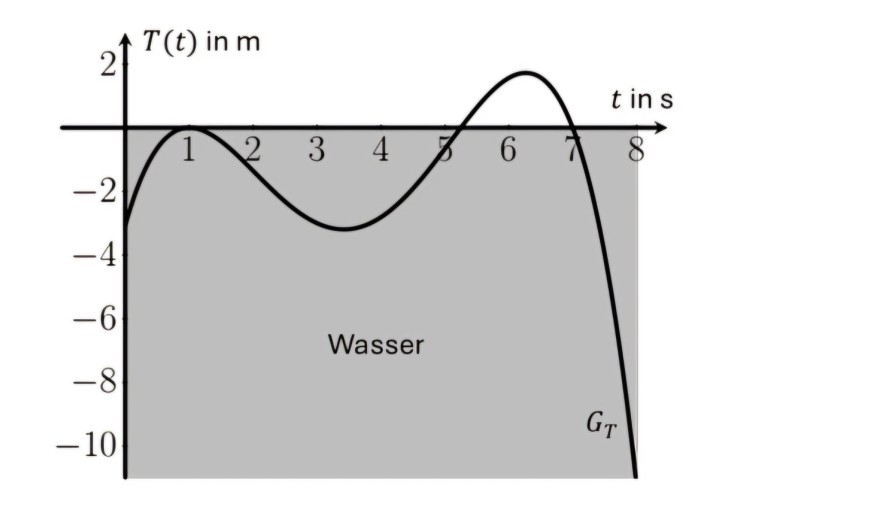
Das Auf- und Abtauchverhalten eines Delfins im Meer wird mittels eines an ihm angebrachten Sensors untersucht. Die momentane Höhe des Sensors in Metern bezogen auf die Wasseroberfläche in Abhängigkeit von der Zeit t in Sekunden lässt sich annähernd durch die Funktionswerte der Funktion T beschreiben. Der Graph der Funktion T wird mit G_T bezeichnet und ist im Zeitraum von 0 bis 8 Sekunden im nebenstehenden Koordinatensystem abgebildet. Die Funktion ist eine ganzrationale Funktion vierten Grades und zum Zeitpunkt t₁=1 befindet sich der Delfin an der Wasseroberfläche.

Die Funktion ist gegeben durch die Funktionsgleichung f(x)=−1/12 * (t⁴ -43/3t^{3 +} 63t²  - 87t + 112/3)

Berechenen sie wie lange der Delfin an der Wasseroberfläche ist  um Luft zu holen.

Problem/Ansatz:

Meine Ideen wäre Nullstelle bestimmen und dan eine Ungleichung wann die Funktion größer als 0 ist aber ich weiß nicht wie ich das angeben kann, wie lange der oben ist.

@Apelmännchen oder @Mathecoach vielleicht wisst ihr wie das geht?

Comments

Das weiß natürlich hier fast jeder. Aber wenn Du lieber auf einen der Kollegen:innen warten willst....

---

Die Antworten unterscheiden sich nun einmal stark in ihrer Qualität. Nachvollziehbar finde ich das also schon. Ich fühle mich geehrt. Danke. :)

Answer 1

Da in der Aufgabe berechnen steht, gehe ich davon aus, dass ein Näherungsverfahren oder der Taschenrechner hier nicht das Hilfsmittel der Wahl ist. Anhand der Abbildung kann man die Nullstellen 1 und 7 ablesen. Und 1 sogar als doppelte Nullstelle (siehe Aufgabenstellung). Prüfe bitte rechnerisch, ob 7 auch eine Nullstelle ist (einsetzen und es muss 0 rauskommen). Dann kannst du mit Hilfe der Polynomdivision bzw. des Horner-Schemas (sofern bekannt), zweimal durch \((x-1)\) (weil doppelte Nullstelle) bzw. \((x-7)\) dividieren und erhältst dann ein Polynom von Grad 2, dessen weiteren Nullstellen du mit der pq-Formel berechnen kannst oder wenn du 3 mal Polynomdivision machst sogar von Grad 1.

Die Differenz der dritten minus der zweiten Nullstelle ist dann die gesuchte Zeit. Dass in diesem Intervall der Delfin oberhalb der Wasseroberfläche ist, kann man entweder mit Hilfe der Abbildung begründen oder man zeigt z.B., dass \(f(6)>0\) gilt.

Answer 2

Nullstellen ist gute Idee, Ungleichung nicht. Gesucht wird die Länge der orangen Strecke.

Comments

Ungleichung nicht.

Geht dann auch eine Vorzeichentabelle, wo ich dann sehen kann in welchem Intervall die Funktion >0, weil wo der Delfin Luft holt ist er ja oberhalb der x Achse also größer als 0?

---

Das ist nicht nötig. Es steht ja bereits in der Aufgabe, wo der Wert >0 ist.

Answer 3

\(f(x)=−\frac{1}{12} * (t^4 -\frac{43}{3}t^3 + 63t^2  - 87t + \frac{112}{3})\)
zum Zeitpunkt \(t_1=1\) befindet sich der Delfin an der Wasseroberfläche:
→ Danach ist er wieder unter der Wasseroberfläche.
Demnach ist zum Zeitpunkt \(t_1=1\) ein Maximum zu erwarten. Somit existiert bei \(t_1=1\) eine doppelte Nullstelle. Den Faktor \((t-1)^2\) kannst du nun abspalten und weitere Nullstellen finden. Die Zeit zwischen den Nullstellen ist nun die Auftauchzeit.

Comments

Das sind weniger als 2 Sekunden. Man sieht sehr deutlich, dass bei 5 keine Nullstelle ist.

---

Hat sich geklärt Danke