Zeigen Sie, dass für n ∈ N mit n≥6 gilt

Question

Aufgabe:

Zeigen Sie, dass für n ∈ N mit n≥6 gilt

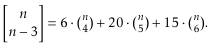
Text erkannt:

\( \left[\begin{array}{c}n \\ n-3\end{array}\right]=6 \cdot\binom{n}{4}+20 \cdot\binom{n}{5}+15 \cdot\binom{n}{6} \).

Problem/Ansatz:

Ich finde hier keinen Ansatz oder Berechnung dazu, unser Prof hat es nicht in der Vorlesung behandelt

und in der Übung haben wir 2 und 3 er Zykel und n-2, n-3  1er Zykel notiert die wir benutzen sollen, habe ich hab trotzdem keine Durchblick. Über Hilfe würde ich mich freuen.

Comments

unser Prof hat es nicht in der Vorlesung behandelt

Willkommen auf der Uni oder FH. Das läuft eben nicht mehr so wie in der Schule. Es geht in den Übungsaufgaben darum, sich intensiver mit der Thematik auseinanderzusetzen. Dazu muss man dann schonmal etwas tüfteln oder anderweitig recherchieren.

---

Ach ist das an den Unis so, ist mir nicht aufgefallen. Wenn ich es probiert und verstanden und hinbekommen hätte, würde ich diese Frage nicht hier stellen, oder ? sieht wohl danach aus, dass ich es nicht hinbekommen habe. Vielen Dank

---

Hallo Hanbei. Die runden Klammern rechts vom Gleichheitszeichen sind Binomialkoeffizienten. Was ist die eckige Klammer links vom Gleichheitszeichen? Hast du mir dafür eine Definition?

---

10 Tage ohne Antwort. Der Fragesteller ist nicht weiter interessiert.