Rentenbarwert zu Pensionsnatritt

Question

Sie haben eine Pensionsvorsorge abgeschlossen, die Ihnen ab Pensionsantritt eine wertgesicherte, jährliche Rente für 13 Jahre zusichert. Es wird angenommen, dass die erste Rentenzahlung in Höhe von 30.000 Euro zum Zeitpunkt des Pensionsantritts in t=25 erfolgt, und dass insgesamt genau 13 Zahlungen stattfinden. Der Kalkulationszinssatz beträgt 3,6 Prozent p.a. bei jährlicher Verzinsung und die Wertsicherung beträgt 0,5 Prozent pro Jahr.

Lösung ist: Der heutige Wert der Pensionsvorsorge beträgt 135.117,20 Euro

Hab diese Formel verwendet: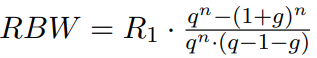

RBW= 30000*((1,036^25-1,005^25)/(1,036^25*(1,036-1-0,005))

Ich komme aber nicht auf 135k

Answer 1

30.000*\( \frac{1,036^{13}*1,005^{13}}{1,036-1,005} \)  = \( \frac{500.059,39}{1,036^{(13+24)}} \)  =  135.117,20

Answer 2

Barwert der Rente:

30000*1,036(1,036^13-1,005^13)/(1,036-1,005)*1/1,036^38 = 135117,20

a) Es werden nur 13 Renten bezahlt, vorschüssig

b) Du musst um 38 Jahre auf heute abzinsen.

Meine Formel:

R*q*(q^n-d^n)/(q-d) * 1/q^{n+a}

d= Dynamikfaktor, a = Beginn der Rente nach a Jahren