Text erkannt:
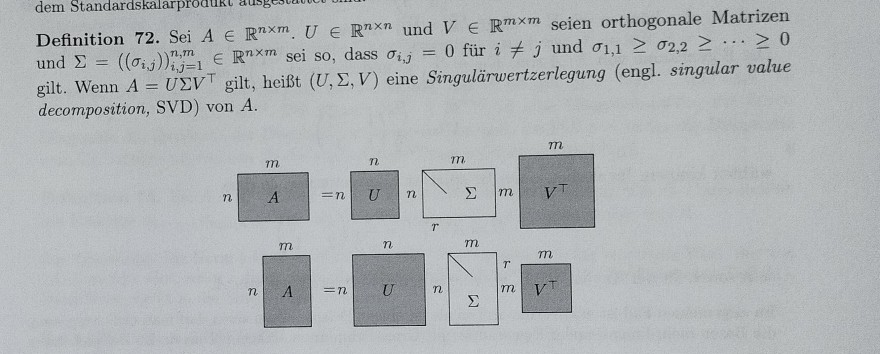
Definition 72. Sei \( A \in \mathbb{R}^{n \times m} . U \in \mathbb{R}^{n \times n} \) und \( V \in \mathbb{R}^{m \times m} \) seien orthogonale Matrizen und \( \Sigma=\left(\left(\sigma_{i, j}\right)\right)_{i, j=1}^{n, m} \in \mathbb{R}^{n \times m} \) sei so, dass \( \sigma_{i, j}=0 \) für \( i \neq j \) und \( \sigma_{1,1} \geq \sigma_{2,2} \geq \cdots \geq 0 \) gilt. Wenn \( A=U \Sigma V^{\top} \) gilt, heißt \( (U, \Sigma, V) \) eine Singulärwertzerlegung (engl. singular value decomposition, SVD) von \( A \).
Da müsste alles drinnenstehen, was du wissen möchtest :)