Bestimmen Sie für Matrizen alle Eigenwerte λ ∈ K, sowie eine Basis der zugehörigen Eigenräume E(λ)

Question

Aufgabe:

Bestimmen Sie für Matrizen alle Eigenwerte λ ∈ K, sowie eine Basis der zugehörigen Eigenräume E(λ) in den Fällen

K = R und K = C. Wann ist jeweils die Matrix diagonalisierbar, wann nur trigonalisierbar
und wann nicht trigonalisierbar?

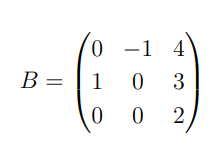
Text erkannt:

\( B=\left(\begin{array}{ccc}0 & -1 & 4 \\ 1 & 0 & 3 \\ 0 & 0 & 2\end{array}\right) \)

Problem/Ansatz:

Ich weiß wie man Eigenwerte und Eigenräume berechnet (Ist der EIgenvektor nicht eine Basis gleich vom Eigenraum?)

Was ist der unterschied zwischen K = R und K = C? K = R, reellen Vektorraum (VR über R), K = C, komplexen Vektorraum (VR über C). Ich weiß, dass es R eigentlich in C enthalten ist, aber weiß nicht, was jetzt bei der Aufgabe der unterschied beim Berechnen wäre.

Answer 1

Ist der EIgenvektor nicht eine Basis gleich vom Eigenraum?

Nein. Es gibt mehrdimensionale Eigenräume. Bei denen besteht die Basis nicht nur aus einem Vektor.

Was ist der unterschied zwischen K = R und K = C

Das charakteristische Polynom hat in \(\mathbb{C}\) möglicherweise mehr Nullstellen als in \(\mathbb{R}\).

Comments

Und wie wirkt sich das aufs rechnen aus?

---

Die Matrix \(B\) hat den reellen Eigenwert \(\lambda_0\).

Polynomdivision des charakteristischen Polynoms durch \(x-\lambda_0\) liefert das Polynom \(-x^2 - 1\).

Dieses Polynom hat in \(\mathbb{R}\) keine Nullstellen. Also hat \(B\) für \(K = \mathbb{R}\) nur diesen einen Eigenwert.

In \(\mathbb{C}\) hat \(-x^2 - 1\) aber zwei Nullstellen. Also hat \(B\) für \(K = \mathbb{C}\) insgesamt drei Eigenwerte.

---

wenn der Eigenraum eindimensional ist, ist dann der eigenvektor die basis

---

Wenn der Eigenraum eindimensional ist, dann ist der Eigenvektor die Basis.

---

Warum hat es in R keine Nullstellen? meinst du mit "nur diesen einen Eigenwert" λ₀ ? Wie komme ich auf dieses ?

---

Warum hat es in R keine Nullstellen?

Weil die Gleichung \(-x^2-1 = 0\) in \(\mathbb{R}\) keine Lösung hat.

meinst du mit "nur diesen einen Eigenwert" λ₀ ?

Ja.

Wie komme ich auf dieses ?

So wie man häufig auf Eigenwerte kommt: Eigenwerte sind genau die Nullstellen des charakteristischen Polynoms.

---

Ahh die die umformung ist -(x-i)+(x+i) Diese Nullstellen i und -i existieren nur in C und sind da Eigenwerte. Jetzt fehlt mir nur noch das Verständnis wie ich λ₀  Herbekomme , dass ist ja von beidem ein Eigenwert. und keine Nulstelle. Wie komme ich dann auf die Basen der eigenräume wenn eigenewerte i und -i sind?

---

Und hier mal zum verständnis:

Text erkannt:

\( A=\left(\begin{array}{cccc}1 & 0 & 0 & 0 \\ -4 & 1 & 0 & 3 \\ 2 & 2 & 1 & 0 \\ 10 & 0 & 0 & -1\end{array}\right) \)

wenn ich diese matrix habe, ist das Charakteristisches Polynom λ4 - 2λ3 + 2λ - 1

-1,1,1,1 Die eigenwerte und sind Somit alle in R und hat aber auch in C dann die gleichen Eigenwerte oder ? Und die die eine Dimension des Eigenraumes ist 3 und die andere 1

---

-(x-i)+(x+i)

-(x-i)·(x+i)

wie ich λ₀ Herbekomme

Nullstelle des charakteristischen Polynoms.

Hast du mittlerweile das charakteristische Polynom bestimmt?

Wie komme ich dann auf die Basen der eigenräume wenn eigenewerte i und -i sind?

Die Eigenräume sind eindimensional. Also ganz normal Eigenvektor bestimmen.

---

λ3 - 2λ2 + λ - 2

Also ist 2 Der Eigenwert den ich suche

---

Das ist richtig. Im reellen Fall ist das der einzige. Im komplexen Fall kommen noch i und -i dazu.

---

Okay also sind die Basen von B:

-i =(-i,1,0)

i=(i,1,0)

2= (1,2,1)

---

Und die die eine Dimension des Eigenraumes ist 3 und die andere 1

Die Vielfachheit der Nullstelle des charakteristischen Polynoms nennt man algebraische Vielfachheit.

Die Dimension des dazugehörigen Eigenraumes nennt man geometrische Vielfachheit.

Diese zwei müssen nicht gleich sein, aber die geometrische Vielfachheit ist nicht größer als die algebraische Vielfachheit.

Um den Eigenraum von \(A\) zum Eigenwert \(-1\) zu bestimmen, löse die Gleichung

        \(A\cdot \begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix} = -1\cdot \begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}\)

---

Warum ist bei -1  Der eigenvektor nicht der eigenraum, es ist doch nur eine 1 fache Nullstelle bei 1 ist es was anders eine Dreifache,

---

War nur ein Beispiel. Für den Eigenwert 1 wird der Eigenraum entsprechend berechnet.

---

Ich hab jetzt alles verstanden außer die Basis zum Eigenwert 1 im Dreidimensionalen Raum.

\( A=\left(\begin{array}{cccc}1 & 0 & 0 & 0 \\ -4 & 1 & 0 & 3 \\ 2 & 2 & 1 & 0 \\ 10 & 0 & 0 & -1\end{array}\right) \) 

1x₁+0x₂+0x₃+0x₄=1x₁

-4x₁+1x₂+0x₃+3x₄=1x₂

_{So oder war das oben adners gemeinnt?}

---

So war das gemeint. Aber da fehlen noch zwei Gleichungen.

---

Wie beweise ich jetzt das A Triagonal ist aber nicht diagonal ist ohne Jordan