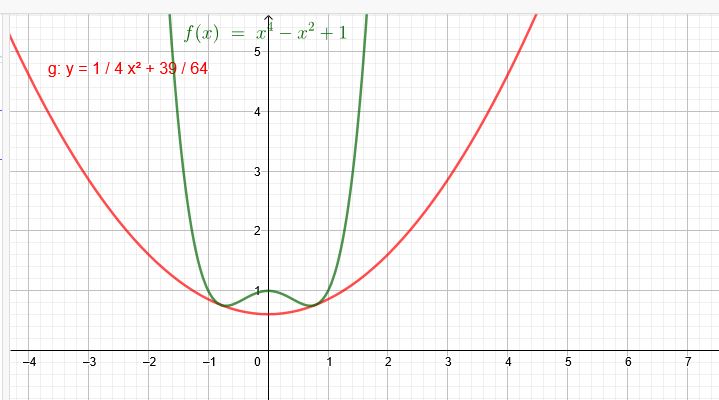
Gegeben ist die Funktion f mit \(f(x) = x^4 - x^2 + 1\)
2.1
Untersuchen Sie den Graphen von f auf Schnittpunkte mit den Koordinatenachsen
Schnitt mit der y-Achse:
\(f(0) =1\)
Schnitt mit der x-Achse:
\( x^4 - x^2 + 1=0\)
\( (x^2 - 0,5)^2 =-1+0,25\)→ kein Schnitt mit der x-Achse
Symmetrie:
Punktsymmetrie ?
\(f(-x)=-f(x)\)
\( (-x)^4 - (-x)^2 + 1 \overset{\text{?}}{\underset{\text{?}}{=}} -(x^4 - x^2 + 1)\)
\( x^4 - x^2 + 1 ≠ -x^4 + x^2 -1)\)
Symmetrie zur y-Achse?
\(f(x)=f(-x)\)
\(f(x) = x^4 - x^2 + 1\)
\(f(-x) = (-x) ^4 - (-x) ^2 + 1=x ^4 - x ^2 + 1\)
Somit liegt eine Symmetrie zur y-Achse vor.
Extrempunkte
\(f'(x) =4x^3 -2x \)
\(4x^3 -2x=0 \)
\(x(4x^2-2)=0 \) Satz vom Nullprodukt:
\(x_1=0\) \(f(0) = 1\) Siehe auch Schnitt mit der y-Achse
\(4x^2-2=0 \)
\(x^2=\frac{1}{2} \)
\(x_2=\frac{1}{\sqrt{2}} \) \(f(\frac{1}{\sqrt{2}}) =\frac{1}{4}- \frac{1}{2}+1= \frac{3}{4}\)
\(x_3=-\frac{1}{\sqrt{2}} \) \(f(-\frac{1}{\sqrt{2}}) = \frac{3}{4}\)
Art der Extremwerte
\(f''(x) =12x^2 -2 \)
\(f''(0) = -2<0 \) Maximum
\(f''(\frac{1}{\sqrt{2}}) =12(\frac{1}{\sqrt{2}})^2-2=4>0 \)Minimum
\(f''(-\frac{1}{\sqrt{2}}) =12(-\frac{1}{\sqrt{2}})^2-2=4>0 \)Minimum
Wendepunkte:
\(12x^2 -2=0 \)
\(x_1=\frac{1}{\sqrt{6}} \) \(f(\frac{1}{\sqrt{6}}) = \frac{1}{36} - \frac{1}{6} + 1=\frac{31}{36}\)
\(x_2=-\frac{1}{\sqrt{6}} \) \(f(-\frac{1}{\sqrt{6}}) =\frac{31}{36}\)
2.2
Berechnen Sie, welches von allen Dreiecken mit den Eckpunkten A (0|9), B (x|f(x)) und C (-x/f(-x)) mit f(x) ≤ 9 maximalen Flächeninhalt hat.
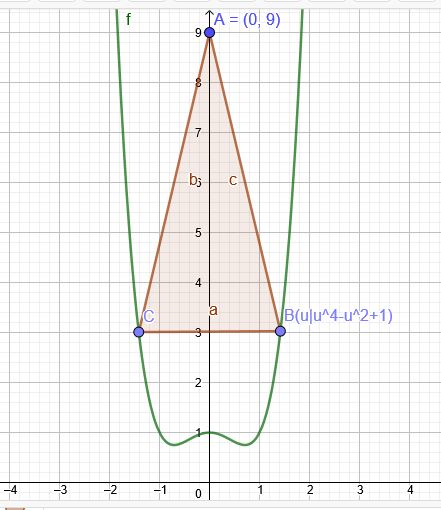
\(A(u)= \frac{1}{2}\cdot 2u \cdot(9-u^4+u^2-1)= (8u-u^5+u^3) \)
\(A'(u)= (8-5u^4+3u^2) \)
\(8-5u^4+3u^2=0 \) \(5u^4-3u^2=8 \) \(u^4-0,6u^2=1,6 \)
\((u^2-0,3)^2=1,6+0,09 =1,69 |±\sqrt{~~}\)
1.)
\(u^2-0,3=1,3 \)
\(u^2=1,6 |±\sqrt{~~}\)
\(u_1=\sqrt{1,6 }\)
\(u_2=-\sqrt{1,6 }\)
2.)
\(u^2-0,3=-1,3 \)
\(u^2=-1 \) keine Lösungen in ℝ
Größtes Dreieck \(A(0|9), B( \sqrt{1,6 }|1,96) , C (- \sqrt{1,6 }|1,96)\)
2.3
Berechnen Sie den Flächeninhalt der Fläche, die der Graph von f mit der Parabel zu \(y = \frac{1}{4} x^2\) einschließt.
\(x^4-x^2+1=\frac{1}{4} x^2\)
Da gibt es keine Schnittpunkte und somit keine eingeschlossene Fläche.
Vielleicht fehlt bei der Parabel noch eine x-freie Zahl.
Ich wähle jetzt mal
\((x^4-x^2+1=\frac{1}{4} x^2+2\)
Schnittpunkte:
\(x^4-\frac{5}{4} x^2=1\)
\((x^2-\frac{5}{8} )^2=1+\frac{25}{64}=\frac{89}{64} |±\sqrt{~~}\)
1.)
\(x^2-\frac{5}{8} = \sqrt{\frac{89}{64}}=\frac{1}{8}\sqrt{89}\)
\(x^2 = \frac{5}{8}+\frac{1}{8}\sqrt{89}\)
\(x_1 = \sqrt{\frac{5}{8}+\frac{1}{8}\sqrt{89}}\)
\(A=\int\limits_{0}^{ \sqrt{\frac{5}{8}+\frac{1}{8}\sqrt{89}}}(x^4 -\frac{5}{4} x^2-1)dx≈|-1,4785|=1,4785\)
Man kann die zu \(y = \frac{1}{4} x^2\) gehörende Parabel so verschieben, dass sie den Graphen von f in zwei Punkten berührt. Bestimmen Sie eine Gleichung der verschobenen Parabel.
Verschobene Parabel:
\(y=\frac{1}{4} x^2+n\)
\(x^4-\frac{5}{4} x^2=n-1\)
\((x^4-\frac{5}{8} )^2=n-1+\frac{25}{64}=n-\frac{39}{64} | ±\sqrt{~~}\)
\(x^4-\frac{5}{8} = | ±\sqrt{n-\frac{39}{64}}\)
Tangente wenn Diskriminate 0:
\(n=\frac{39}{64}\)
Der Graph der Parabel \(y=\frac{1}{4} x^2+\frac{39}{64}\) berührt nun die Parabel 4.Ordnung.