Zeigen sie die folgenden Ungleichungen:
Text erkannt:
Übungsaufgabe 2. (7+8+12+11 Pkt.) Zeigen Sie die folgenden Ungleichungen:
a) \( 2^{n}<n \) ! für alle \( n \in \mathbb{N}_{0} \) mit \( n \geq 4 \),
b) \( \binom{n}{j} \frac{1}{n^{j}} \leq \frac{1}{j!} \) für alle \( n \in \mathbb{N}, j \in \mathbb{N}_{0} \)
c) \( \left(1+\frac{1}{n}\right)^{n} \leq \sum \limits_{j=0}^{n} \frac{1}{j!}<3 \) für alle \( n \in \mathbb{N} \),
d) \( \left(\frac{n}{3}\right)^{n} \leq \frac{1}{3} n \) ! für alle \( n \in \mathbb{N} \).
(Tipp: Verwenden Sie für die zweite Abschätzung in c) die Abschätzung aus a) zusammen mit Satz 1.31(j) und der geometrischen Summenformel aus Satz 1.24. Beachten Sie dabei, dass die Ungleichung aus a) nur für \( n \geq 4 \) gilt.)
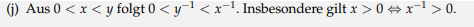
Text erkannt:
(j) Aus \( 0<x<y \) folgt \( 0<y^{-1}<x^{-1} \). Insbesondere gilt \( x>0 \Leftrightarrow x^{-1}>0 \).

Text erkannt:
Satz 1.24 (Geometrische Summenformel).
Für alle \( x \in \mathbb{R} \backslash\{1\} \) und alle \( n \in \mathbb{N}_{0} \) gilt: \( \sum \limits_{k=0}^{n} x^{k}=\frac{1-x^{n+1}}{1-x} \).