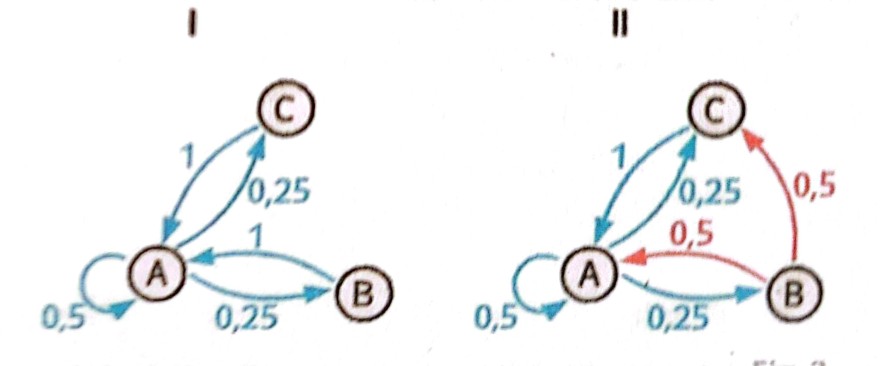
Aufgabe:
a) Bestimmen Sie für das Zustandsdiagramm I eine Übergangsmatrix.
b) Welche Besonderheiten weist dieser Prozess auf?
c) Bestimmen Sie eine stabile Verteilung des Prozesses.
d) Durch Eingriffe von außen verändert sich der Prozess (siehe Zustandsdiagramm II). Begründen Sie ohne Rechnung, wie und in welche Richtung sich die Anteile des Grenzzustandes verändern.
e) Berechnen Sie die Grenzverteilung.
Problem/Ansatz:
Bei a) habe ich die Übergangsmatrix P= \( \begin{pmatrix} 0,5 & 1&1 \\ 0,25 & 0&0 \\ 0,25 & 0 & 0 \end{pmatrix} \)
Aber beim Rest komme ich nicht weiter..