Aufgabe:
Meine Frage ist wie ich von dem Integral auf das bestimmte Integral kommen, ich verstehe nicht ganz wie sich k und j umtauschen.
Problem/Ansatz:
Ich habe es versucht zu berechnen, aber kam nicht weiter, hat jemand einen Rechenweg, damit ich verstehe wie man auf dieses Ergebnis kommt.
Danke im Voraus 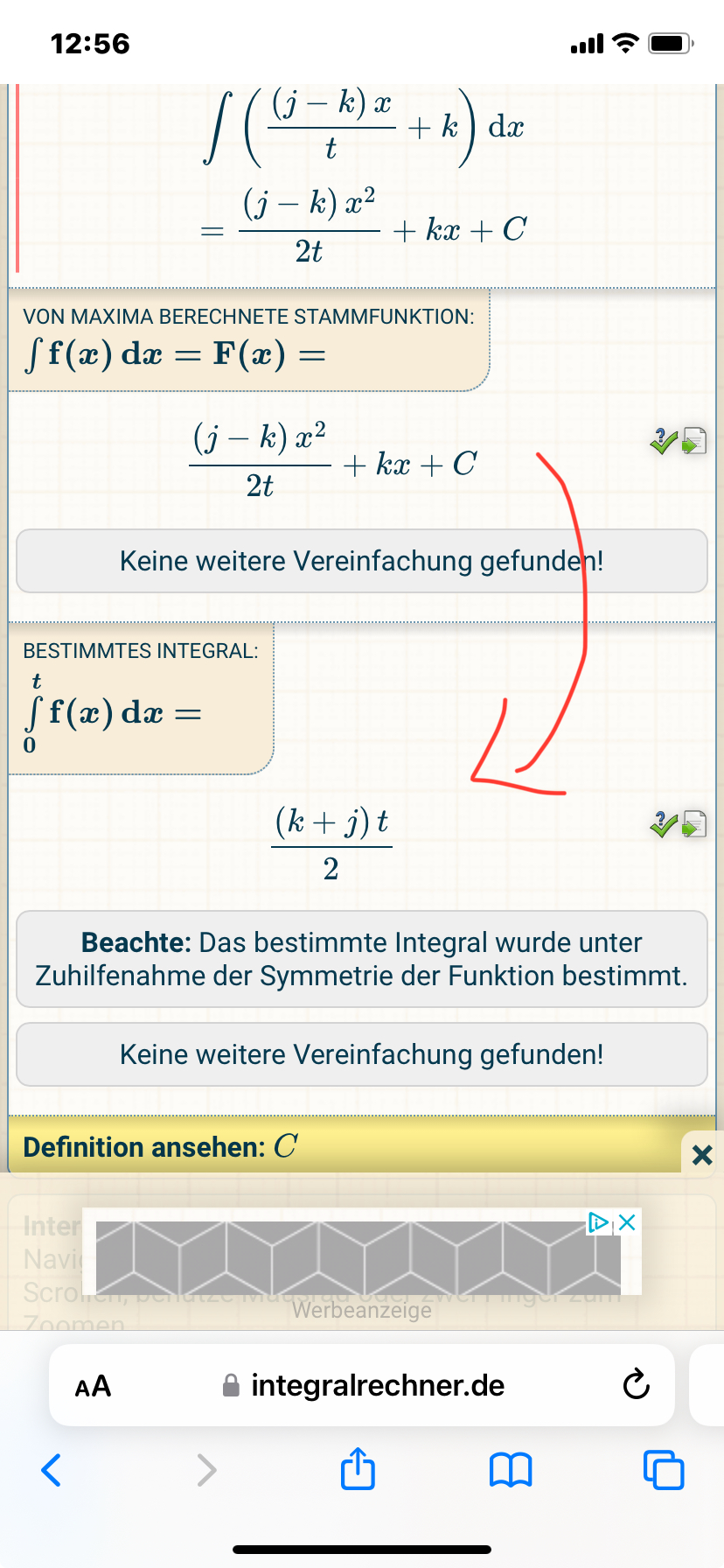
Text erkannt:
12:56
\( \begin{array}{l} \int\left(\frac{(j-k) x}{t}+k\right) d x \\ =\frac{(j-k) x^{2}}{2 t}+k x+C \end{array} \)
VON MAXIMA BERECHNETE STAMMFUNKTION:
\( \begin{aligned} \int \mathbf{f}(\boldsymbol{x}) \mathbf{d} \boldsymbol{x}= & \mathbf{F}(\boldsymbol{x})= \\ & \frac{(j-k) x^{2}}{2 t}+k x+C \end{aligned} \)
Keine weitere Vereinfachung gefunden!
Beachte: Das bestimmte Integral wurde unter Zuhilfenahme der Symmetrie der Funktion bestimmt.
Keine weitere Vereinfachung gefunden!
Definition ansehen: \( C \)
\( A A \) integralrechner.de