Mengen als Vereinigung von Intervallen

Question

Aufgabe:

Schreibe folgende Mengen als Vereinigung von Intervallen und beweise dabei deine Behauptungen.
M1={x∈R:1<x2 +2x≤4}

M2={x∈R:||x+1|−2|≤x}

M3={x∈R:|x+2|>|x−3|

Problem/Ansatz:

Ich bitte um Hilfe

Comments

x2 meint wohl x^2.

M2 /M3 : Fallunterscheidung

Answer 1

Hallo

für M1 löse die 2 ungleichungen, indem due die Gleichungen x^2+2x=1  2 Werte x1,x2  also die Intervalle -oo bis x1 und x2bis oo für die linke Ungleichung,   und x^2+2x=4  2 Werte  jetzt kleiner

am einfachsten ist es die Parabel x^2+2x zu skizzieren und mit den Geraden y=1 und y=4 zu schneiden dann sieht man die Lösungsmenge, das offene Intervall direkt.

bei M2 und M3 brauchst du Fallunterscheidungen 1. |x+1|>2 und |x+1| <2 um den äußere Betrag zu entfernen  , dann noch x+1>0 und x+1<0

also mach dich mal an die Arbeit, auch hier hilft es y= ||x+1|-2| und y=x 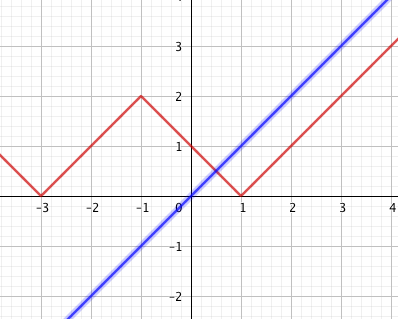zu skizzieren das zeig ich mal :

Gruß lul

Comments

Ich bitte um die Lösung zum Abgleich. Vielen Dank